Metode Numerik adalah teknik untuk menyelesaikan permasalahan-permasalahan yang diformulasikan secara matematik dengan cara operasi hitungan (arithmetik).Teknik ini diperlukan karena tidak semua permasalahan matematis dapat diselesaikan dengan mudah secara analitik bahkan ada yang sama sekali tidak dapat diselesaikan secara analitik. Jika suatu persoalan sudah sangat sulit atau tidak mungkin diselesaikan dengan analitik maka alternatifnya adalah mencari penyelesaian pendekatan dengan metode numerik. Karena penyelesaian yang dihasilkan berupa nilai pendekatan maka tentu ada error dari penyelesaian yang dihasilkan.

Dalam metode numerik, pencarian akar f(x) = 0 dilakukan secara iteratif (looping).Secara umum metode pencarian akar dapat dikelompokkan menjadi dua jenis , yaitu ;Metode Tertutup (Bracketing Method) dan Metode Terbuka. Metode yang pertama disebut juga metode pengapitan akar (bracket), oleh karena pencarian akar dilakukan pada suatu interval tertutup [a, b] sedemikian sehingga f(a) dan f(b) mempunyai tanda yang berlawanan. Metode tertutup terdiri atas :

Metode Bisection (Bagi-dua)Metode Regulasi FalsiMetode terbuka merupakan metode yang menggunakan satu atau dua tebakan awal yang tidak memerlukan rentang sejumlah nilai. Metode terbuka terdiri dari beberapa jenis yaitu:

Metode Iterasi Titik TetapMetode Newton-RaphsonMetode SecantDisini kita akan membahas dan menerapkan 4 metode untuk mencari akar-akar Persamaan non-linear. Agar dapat memudahkan perhitungan, kita akan menggunakan software Scilab. Dalam setiap Metode Akan ditampilkan kode program yang akan digunakan untuk melakukan perhitungan numerik yang sesuai dengan metodenya.

1. Metode Regulasi Falsi

Metode regula falsi adalah metode pencarian akar persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari 2 (dua) titik batas range

Langkah-langkah:

Tentukan nilai awal a dan bCek konvergensi nilai f(a) dan f(b)·       Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnya

Jika tanda f(a) = tanda f(b), pilih nilai awal yang baruLakukan iterasi4.    Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))

5.    Cek konvergensi nilai c

·       Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| 

·       Jika nilai Cn dan Cn-1 konstan

·       Jika nilai f(Cn) = 0

6.    Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

·       Jika tanda f(c) = tanda f(a) maka c akan menggantikan a

·       Jika tanda f(c) = tanda f(b) maka c akan menggantikan b

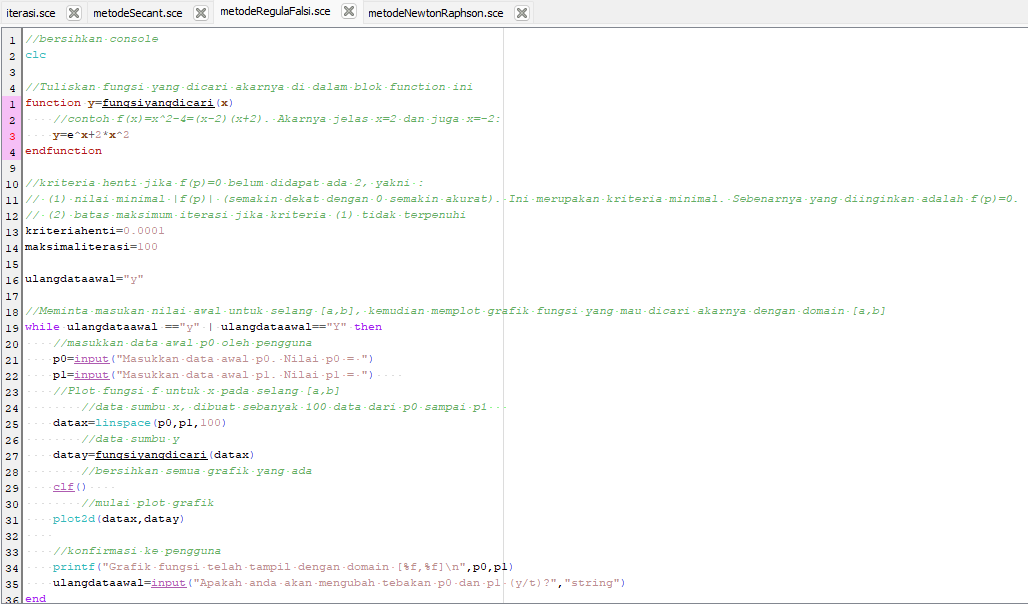
Perhitungan dengan menggunakan Scilab:

 

 

 

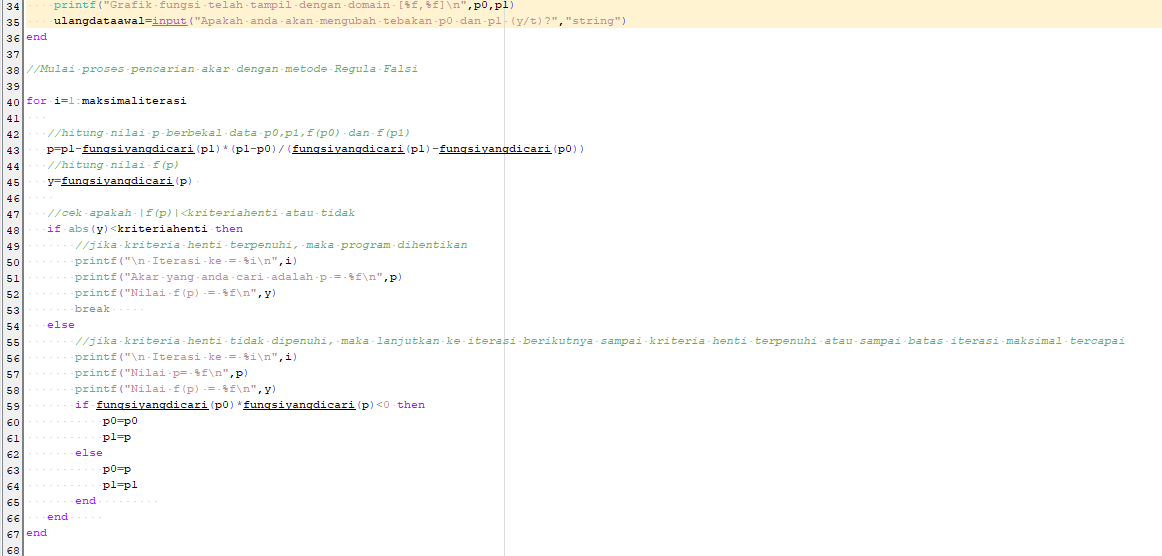
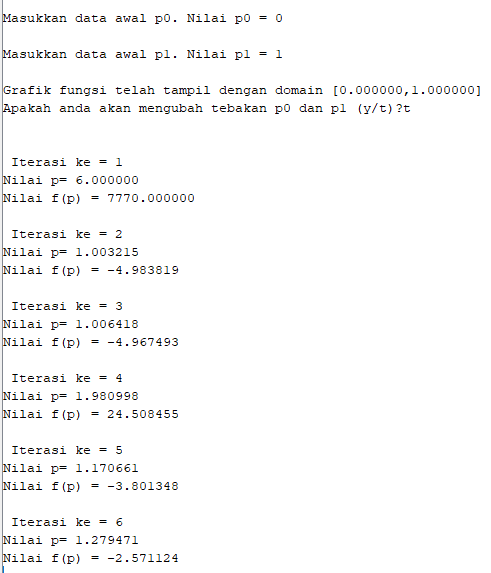
Hasil Program

 

 

2. Metode Secant

Metode Secant merupakan perbaikan dari metode regula-falsi dan Newton Raphson, dimana kemiringan dua titik dinyatakan secara diskrit dengan mengambil bentuk garis lurus yang melalui satu titik.

Langkah-langkah Metode Secant:

a. Tentukan nilai awal x0 dan x1

b. Hitung f(x0) dan f(x1) kemudian cek konvergensi f(x0) dan f(x1)

c. Lakukan iterasi

d. Hitung nilai taksiran akar selanjutnya

           xn+1 = xn - f(xn) × (xn - xn-1)/(f(xn) - f(xn-1))

e. Cek konvergensi terhadap XTOL (Jika ada)

Berikut kode program scilab yang dapat digunakan :

 

 

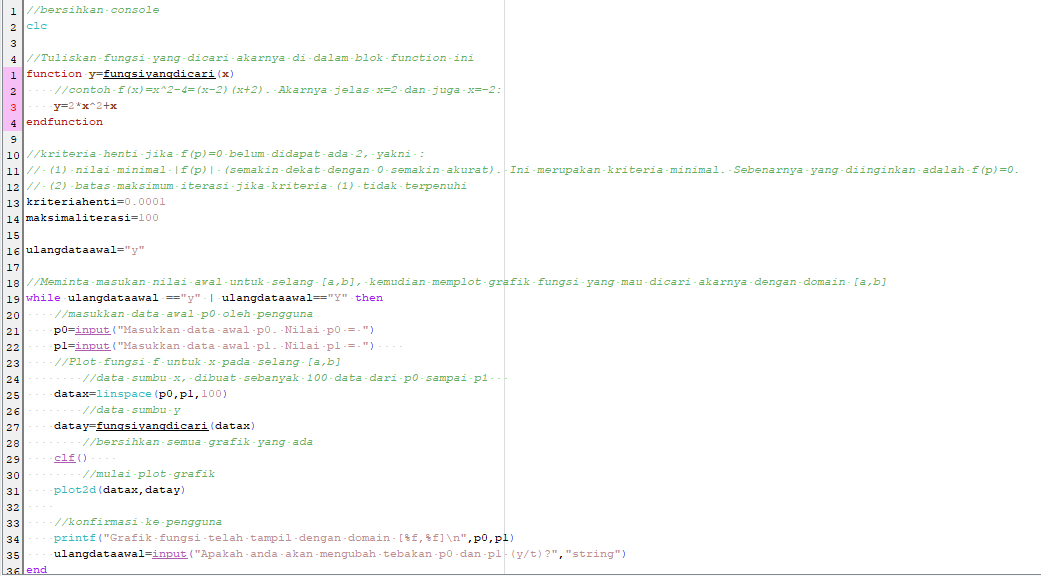
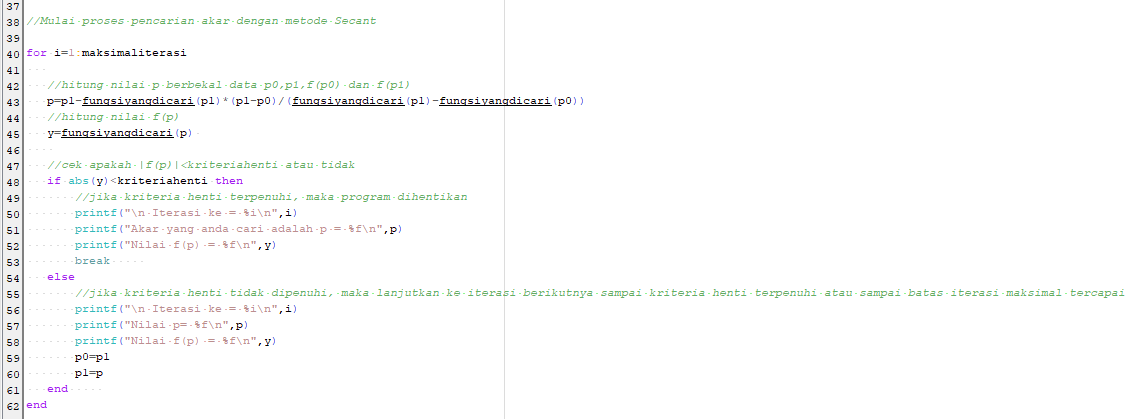
Hasil Program

 

 

3. Metode Newton-Raphson

Langkah-langkah Metode Newton-Raphson:

a. Tentukan nilai awal x0

b. Hitung f(x0) kemudian cek konvergensi f(x0)

c. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

d. Lakukan iterasi

e. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

f. Cek konvergensi terhadapa XTOL (Jika ada)

Berikut kode program scilab yang dapat digunakan :

 

 

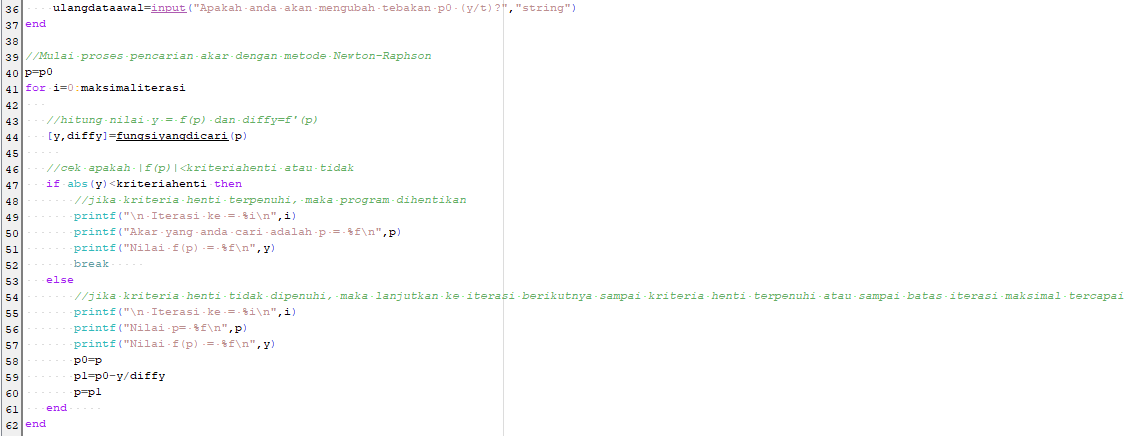
Hasil Program

 

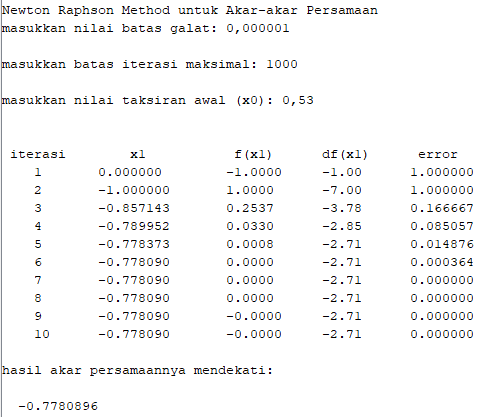
4. Metode Iterasi Titik Tetap

Metode Iterasi Titik tetap kadang-kadang dinamakan metode iterasi sederhana atau metode langsung atau metode substitusi beruntun. Kesederhanaan metode ini karena pembentukan prosedur iterasinya yang mudah dibentuk, yaitu kita ubah persamaan f (x) = 0 menjadi bentuk x = g(x), kemudian dibentuk menjadi prosedur iterasi,Metode iterasi titik tetap termasuk metode terbuka. Artinya dalam menghampiri akar, metode ini tidak memerlukan selang tertutup seperti metode bagi dua dan metode posisi palsu. Kita dapat mentransformasikan fungsi f(x) = 0 dalam bentuk x = g(x). Prosedur iterasi yang berpadanan adalah xn+1 = g(xn) dengan fungsi g seperti yang diperoleh dalam bentuk x = g(x). Suatu selesaian dalam bentuk tersebut disebut suatu titik tetap dari g. Untuk suatu persamaan f(x) = 0 yang diberikan mungkin berpadanan dengan beberapa persamaan x = g(x) akan tetapi bisa menghasilkan kekonvergenan barisan x0, x1, x2, x3, … yang mungkin berbeda, tergantung dari pemilihan x0.Berikut ini langkah penyelesaian Iterasi Titik Tetap:

1.Susunlah persamaan f (x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi: 

xn+1 = g(xn)

2.Tentukan nilai awal x0.

3.Lakukan iterasi dengan menghitung nilai

   x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

 f (k) = 0 ; k = g(k)

4.Cek konvergensi terhadap XTOL (jika ada).

Berikut ini adalah contoh program Scilab:

 

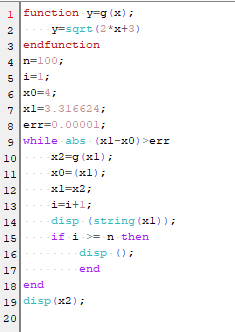
Hasil Program