Masalah menemukan akar dari persamaan nonlinear merupakan masalah yang muncul dalam berbagai disiplin ilmu. Pada realitanya, akar-akar persamaan nonlinear sulit untuk ditemukan secara analitik, kecuali pada kasus-kasus yang lebih sederhana. Oleh karena itu, kita memerlukan sebuah pendekatan secara numerik untuk dapat menyelesaikan masalah yang tidak dapat diselesaikan secara analitik. Hal inilah yang menjadi sebab mengapa metode numerik sangat diperlukan untuk memecahkan persoalan-persoalan dalam bidang sains dan teknologi.

Dalam metode numerik proses pencarian akar dapat dilakukan dalam dua cara, yaitu melalui metode tertutup dan metode terbuka. Metode tertutup disebut juga sebagai metode pengapitan akar, karena proses pencarian akar dilakukan dalam suatu interval tertutup [a,b]. Metode tertutup terdiri atas :

• Metode Bisection
• Metode Regulasi Falsi

Metode terbuka merupakan ssebuah metode yang menggunakan satu atau dua tebakan awal yang tidak memerlukan rentang sejumlah nilai. Metode terbuka terdiri dari beberapa jenis metode, yaitu :

• Metode Secant
• Metode Iterasi Titik Tetap
• Metode Newton Raphson

Di dalam blog ini kita akan membahas dan menerapkan 4 dari 5 metode yang dapat kita gunakan dalam mencari akar-akar persamaan non linear. Agar dapat mempermudah proses perhitungan kita akan memanfaatkan software open source yaitu scilab. Dalam setiap metode akan saya lampirkan kode program yang dapat digunakan untuk melakukan perhitungan numerik yang sesuai dengan metodenya.

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dari dua titik batas range.

Langkah-langkah Metode Regulasi Falsi :

a. Tentukan nilai awal a dan b

b. Cek konvergensi nilai f(a) dan f(b).

• Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnya
• Jika tanda f(a) = tanda f(b), pilih nilai awal yang baru

c. Lakukan iterasi

d. Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))

e. Cek konvergensi nilai c.

• Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| .
• Jika nilai Cn dan Cn-1 konstan
• Jika nilai f(Cn) = 0

f. Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c akan menggantikan a
• Jika tanda f(c) = tanda f(b) maka c akan menggantikan b

Berikut ini kode program scilab yang dapat digunakan :

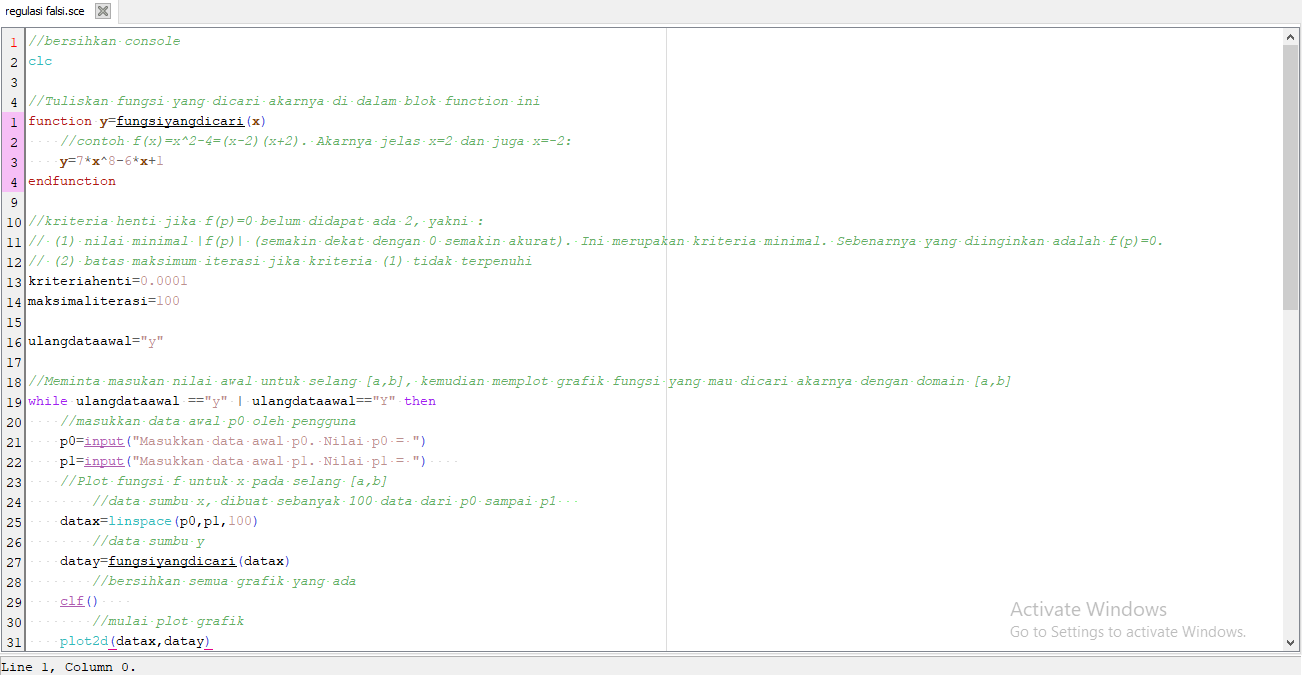
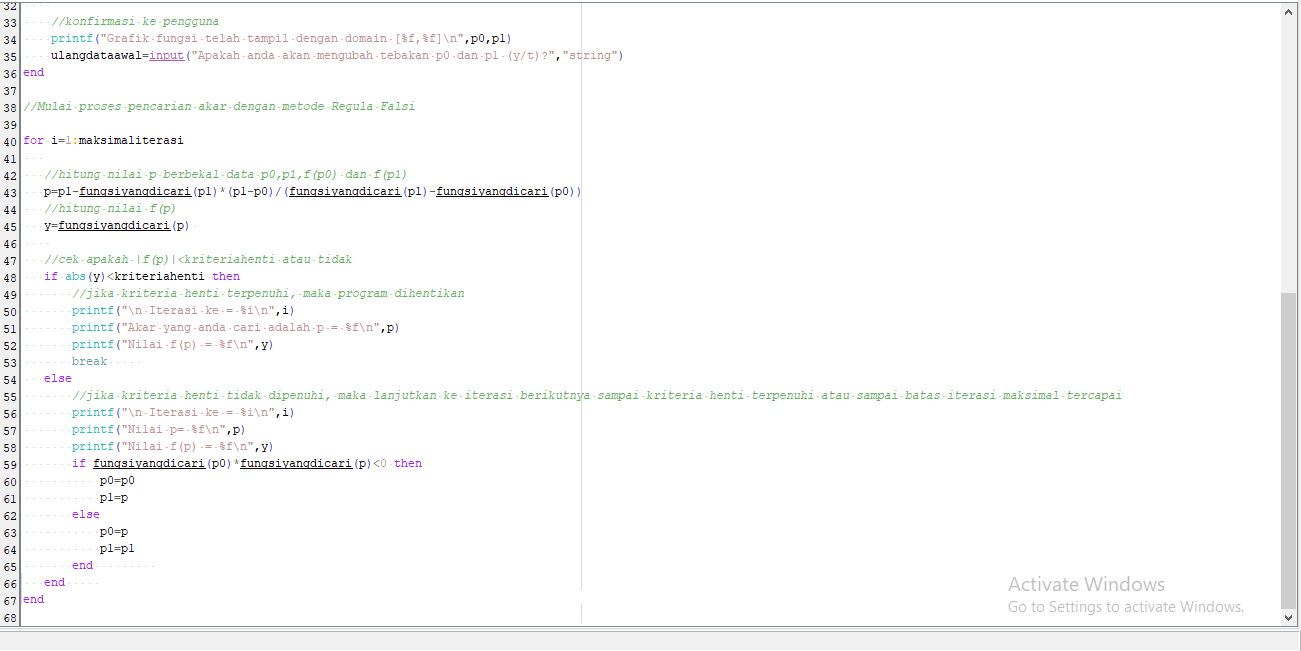
2. Metode Secant

Metode Secant merupakan perbaikan dari metode regula-falsi dan Newton Raphson, dimana kemiringan dua titik dinyatakan secara diskrit dengan mengambil bentuk garis lurus yang melalui satu titik.

Langkah-langkah Metode Secant:

a. Tentukan nilai awal x0 dan x1

b. Hitung f(x0) dan f(x1) kemudian cek konvergensi f(x0) dan f(x1)

c. Lakukan iterasi

d. Hitung nilai taksiran akar selanjutnya

           xn+1 = xn - f(xn) × (xn - xn-1)/(f(xn) - f(xn-1))

e. Cek konvergensi terhadap XTOL (Jika ada)

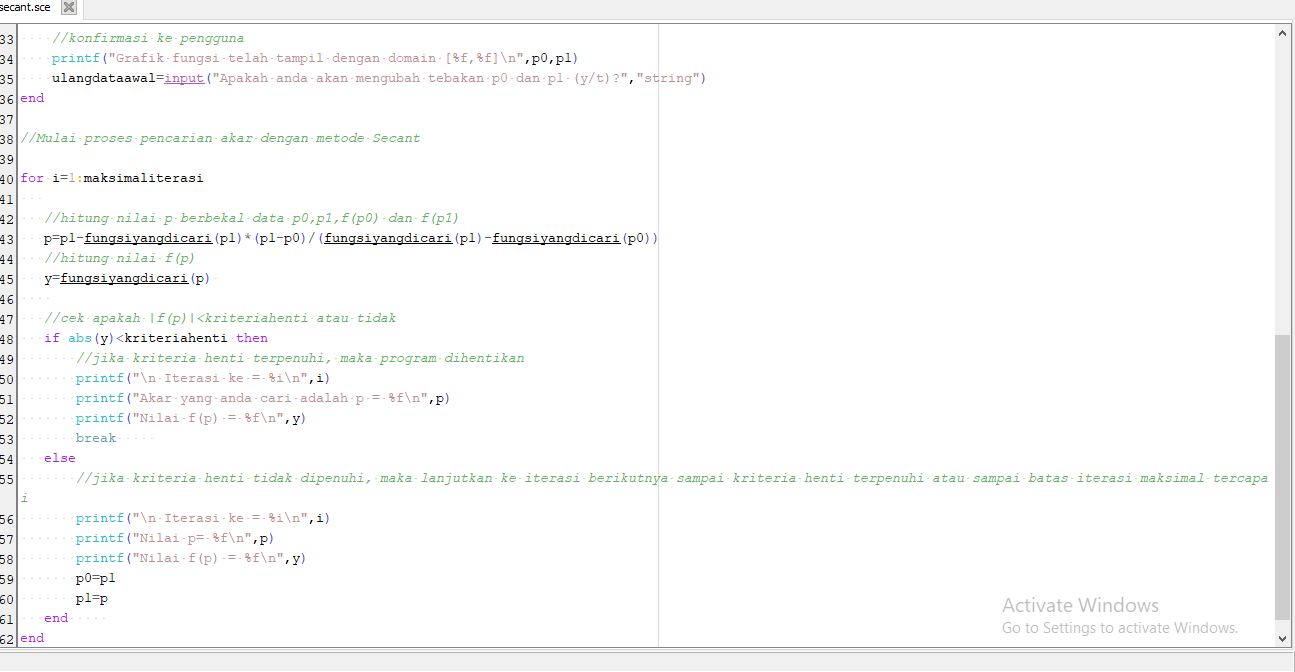
Berikut kode program scilab yang dapat digunakan :

 

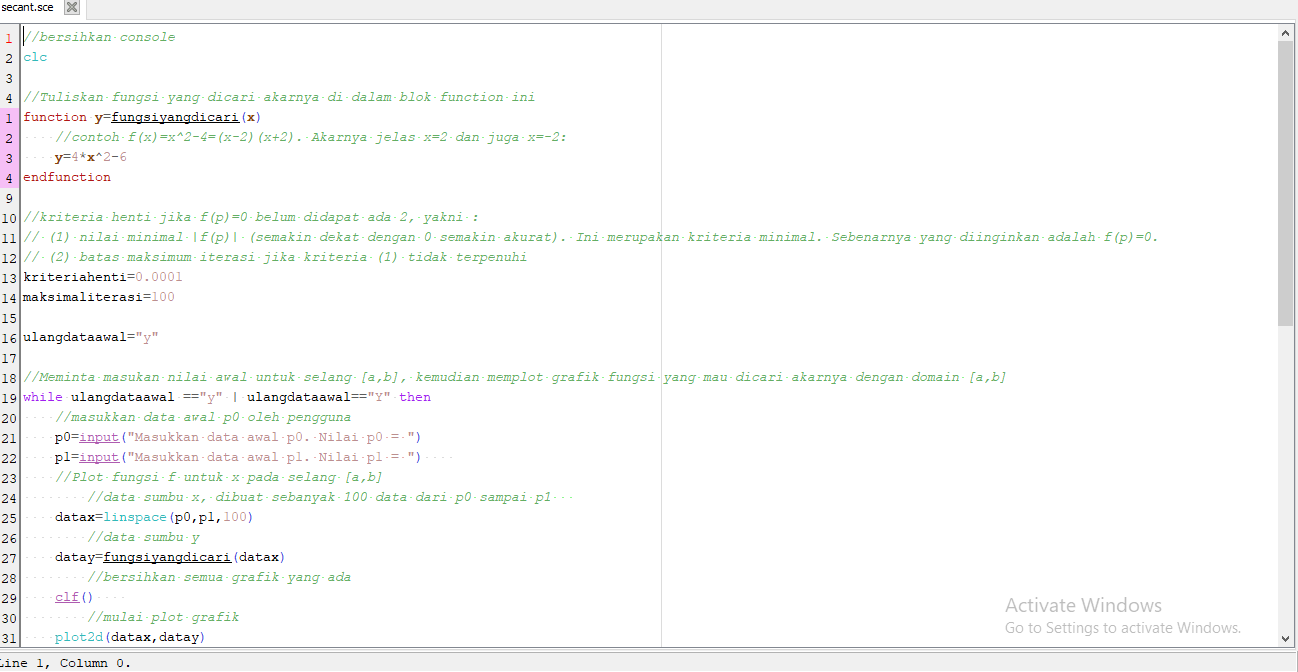
3. Metode Newton Raphson

Langkah-langkah Metode Newton-Raphson:

a. Tentukan nilai awal x0

b. Hitung f(x0) kemudian cek konvergensi f(x0)

c. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

d. Lakukan iterasi

e. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

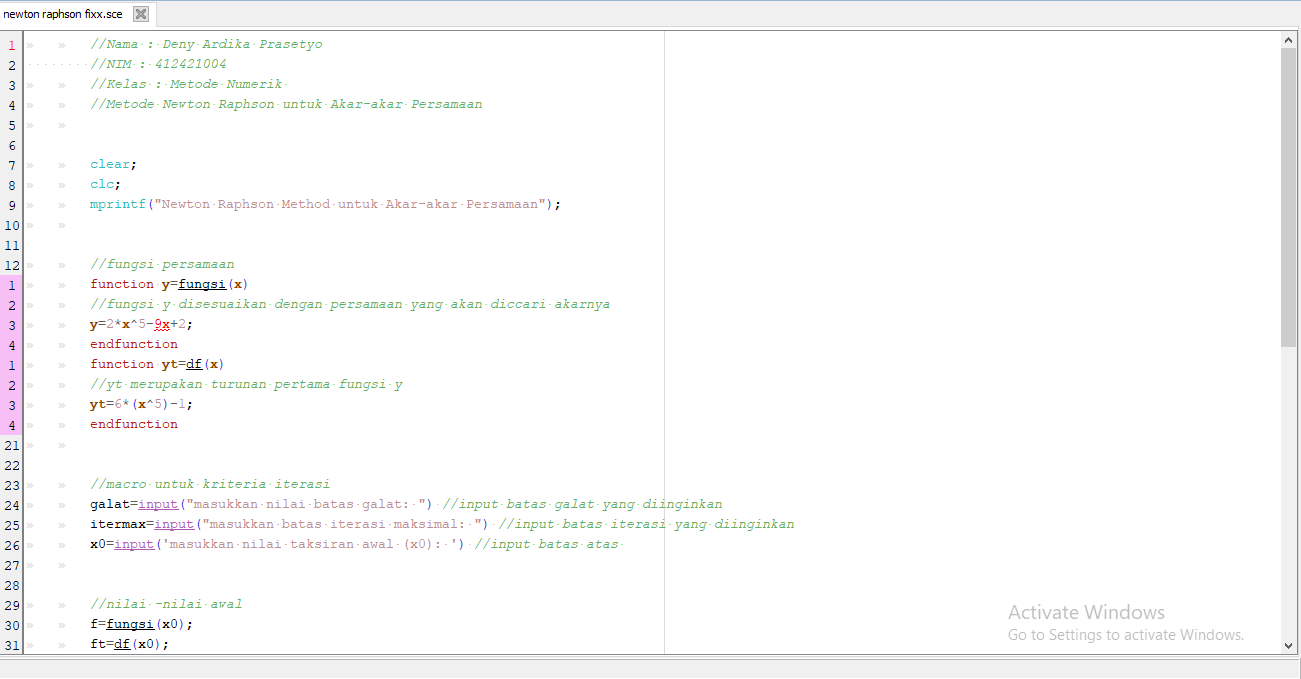
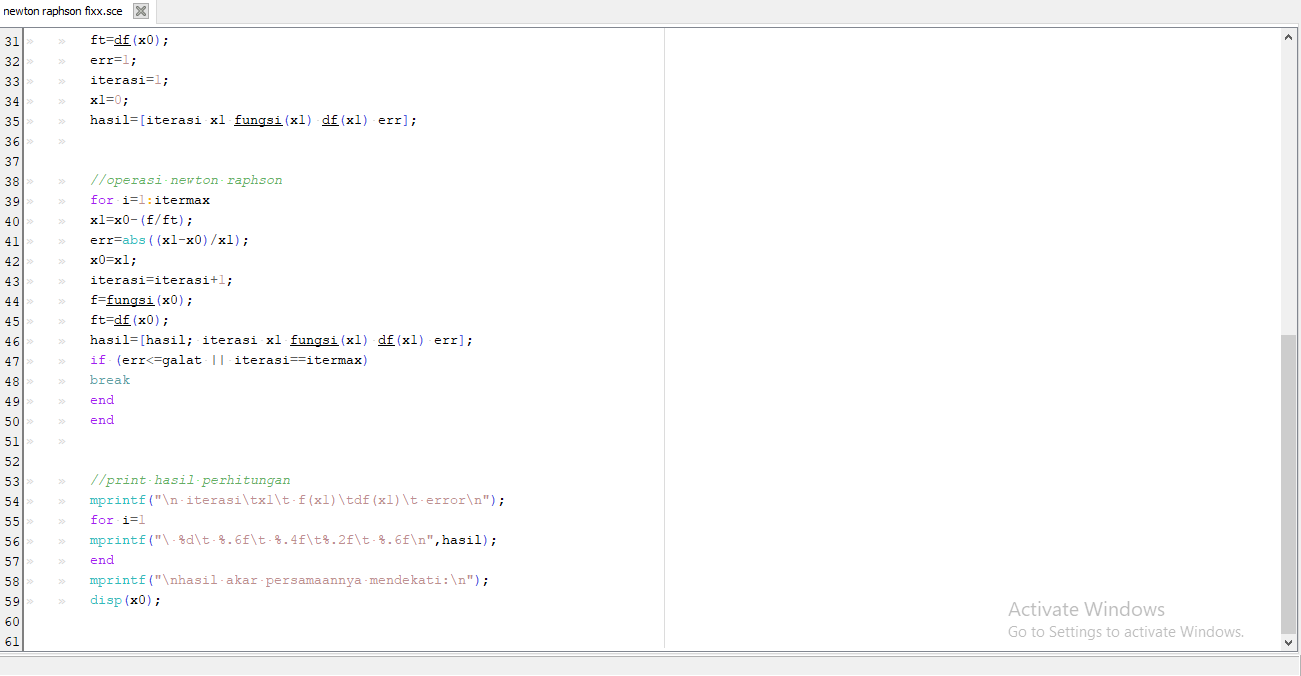
Berikut kode program scilab yang dapat digunakan :

4. Metode Iterasi Titik Tetap

Metode iterasi titik tetap merupakan metode penyelesaian persamaan non-linier dengan cara menyelesaikan setiap variabel xx yang ada dalam suatu persamaan dengan sebagian yang lain sehingga diperoleh x=g(x), x=g(x) untuk masing-masing variabel xx

Langkah-langkah Metode Iterasi Titik Tetap:

a. Susunlah persamaan f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:                             

xn+1 = g(xn)

b. Tentukan nilai awal x0.

c. Lakukan iterasi dengan menghitung nilai x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

f (k) = 0 ; k = g(k)

d. Cek konvergensi terhadap XTOL (jika ada).

 Berikut kode program scilab yang dapat digunakan :