Metode numerik adalah teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan cara operasi hitungan. Dalam metode numerik ini dilakukan operasi hitungan dalam jumlah yang banyak dan prosesnya berulang. Sehingga dalam prakteknya perlu bantuan komputer untuk menyelesaikan hitungan tersebut. Tanpa bantuan komputer, metode numerik tidak banyak memberikan manfaat. 

Metode numerik merupakan alat yang sangat ampuh untuk menyelesaikan permasalahan dalam berbagai bidang. Metode numerik mampu menyelesaikan suatu sistem persamaan yang besar, persamaan yang tidak linier dan persamaan yang kompleks yang tidak mungkin diselesaikan secara analitis. Namun, bisa diselesaikan dengan menggunakan sofwer scilab. Berikut adalah beberapa metode penyelesain:

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dua titik batas jangkauan. Sebenarnya metode ini hampir sama dengan Metode Biseksi, namun titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi.

Langkah-langkah Metode Regulasi Falsi :

1. Tentukan nilai awal a dan b

2. Cek konvergensi nilai f(a) dan f(b)

• Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnya
• Jika tanda f(a) = tanda f(b), pilih nilai awal yang baru

3. Lakukan iterasi

4. Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))

5. Cek konvergensi nilai c

• Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| 
• Jika nilai Cn dan Cn-1 konstan
• Jika nilai f(Cn) = 0

6. Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c akan menggantikan a
• Jika tanda f(c) = tanda f(b) maka c akan menggantikan b

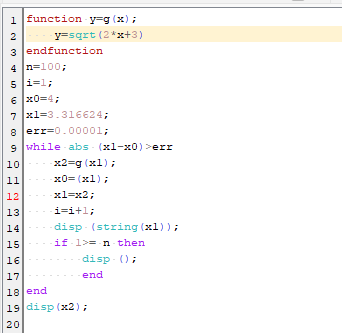
Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Regulasi Falsi :

 

 

 

 

 

 

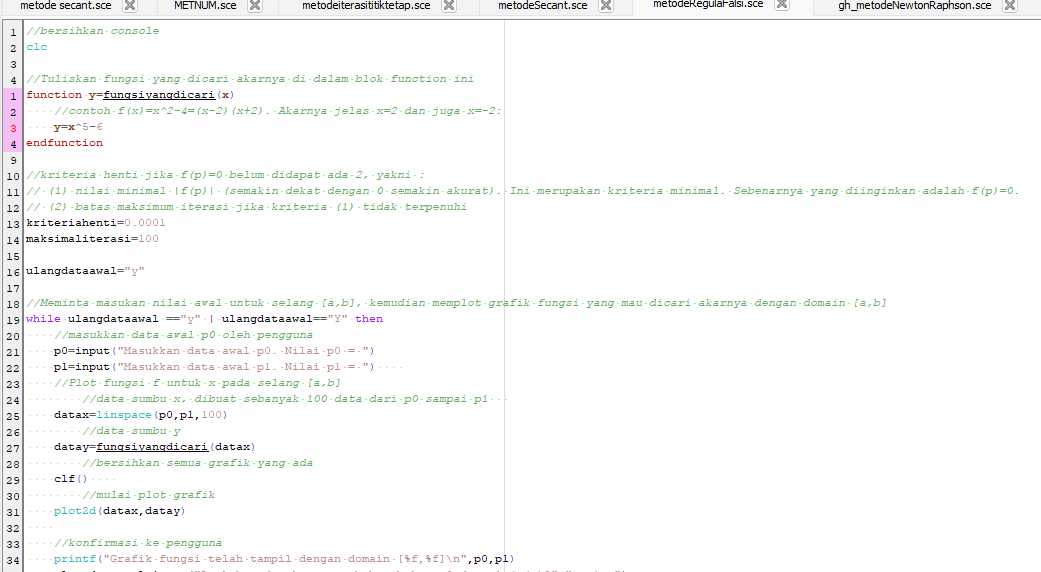
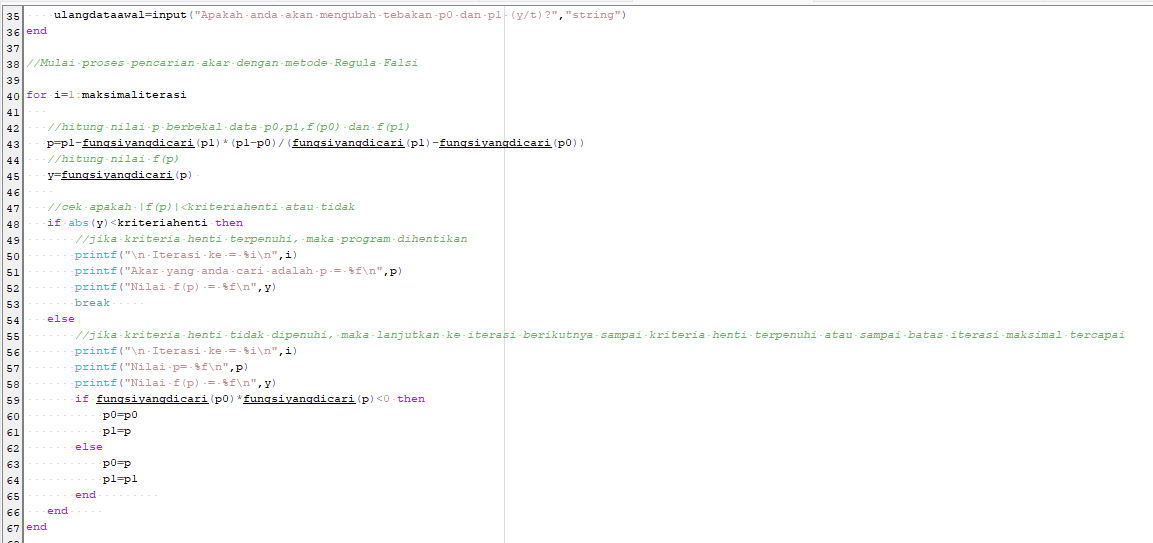
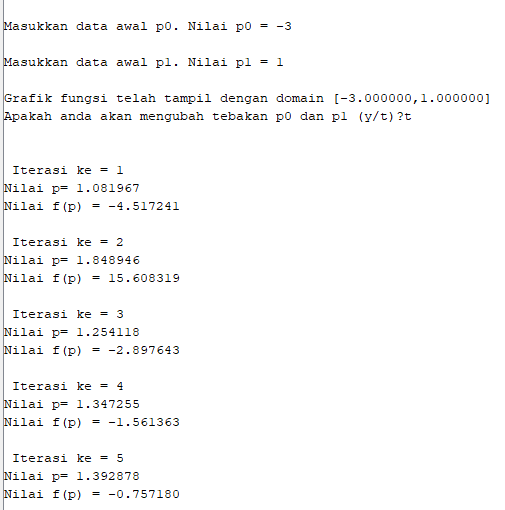
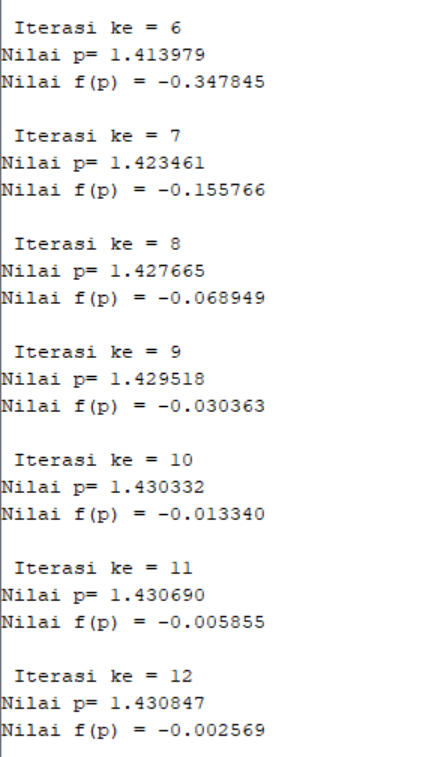
2. Metode Iterasi Titik Tetap

Metode iterasi titik tetap adalah suatu metode pencarian akar suatu fungsi f(x) secara sederhana dengan menggunakan satu titik awal. Metode iterasi titik tetap merupakan metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh x = g(x). 

Langkah-langkah Metode Iterasi Titik Tetap:

1. Susunlah persamaan f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:                             

                          xn+1 = g(xn)

2. Tentukan nilai awal x0.

3. Lakukan iterasi dengan menghitung nilai x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

                        f (k) = 0 ; k = g(k)

4. Cek konvergensi terhadap XTOL (jika ada).

 

Perhitungan menggunakan aplikasi Scilab :

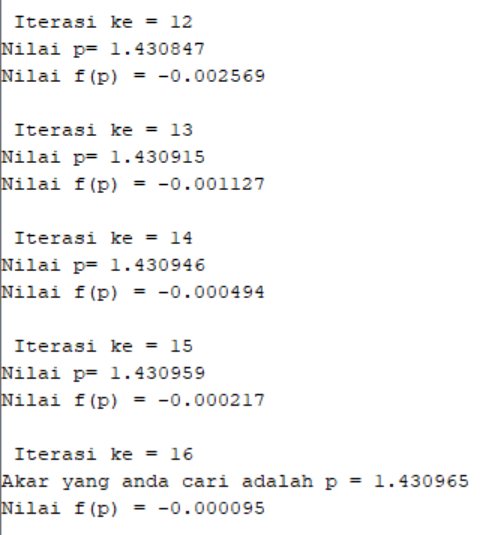
Berikut syntax scilab untuk metode Iterasi Titik Tetap :

 

 

 

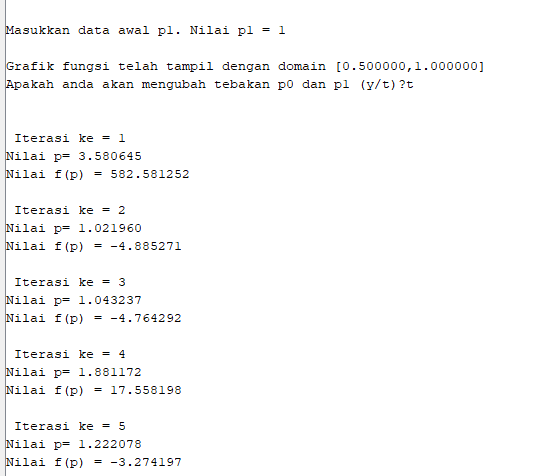
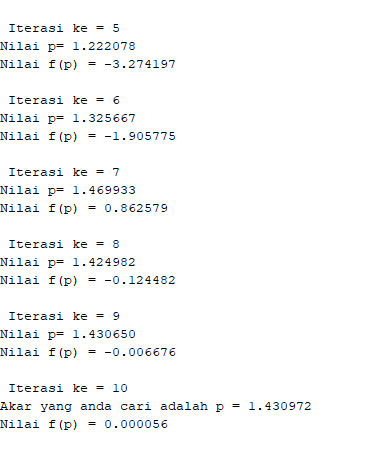
3. Metode Secant

Metode Secant merupakan perbaikan dari metode regula-falsi dan Newton Raphson, dimana kemiringan dua titik dinyatakan secara diskrit dengan mengambil bentuk garis lurus yang melalui satu titik.

Langkah-langkah Metode Secant:

a. Tentukan nilai awal x0 dan x1

b. Hitung f(x0) dan f(x1) kemudian cek konvergensi f(x0) dan f(x1)

c. Lakukan iterasi

d. Hitung nilai taksiran akar selanjutnya

           xn+1 = xn - f(xn) × (xn - xn-1)/(f(xn) - f(xn-1))

e. Cek konvergensi terhadap XTOL (Jika ada)

Berikut kode program scilab yang dapat digunakan :

 

 

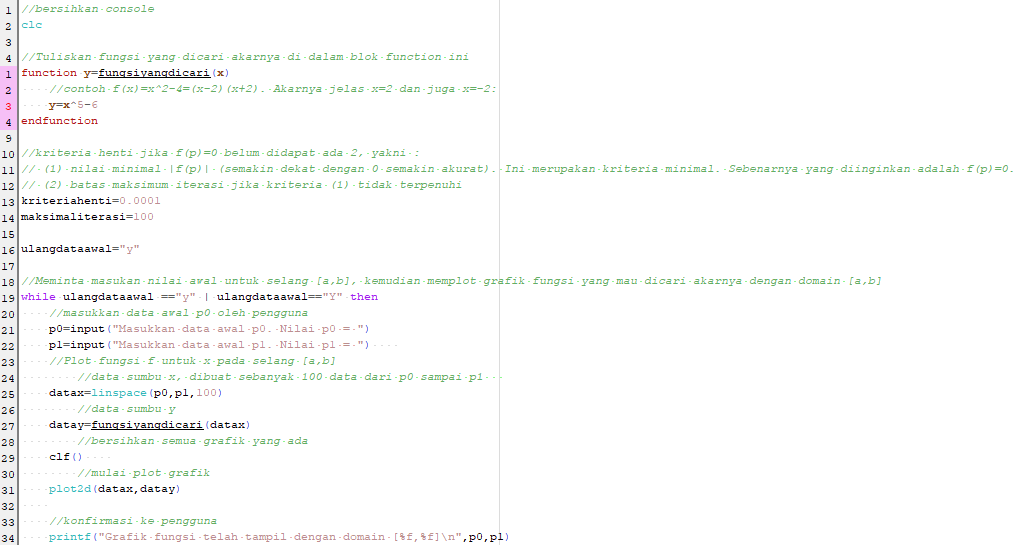
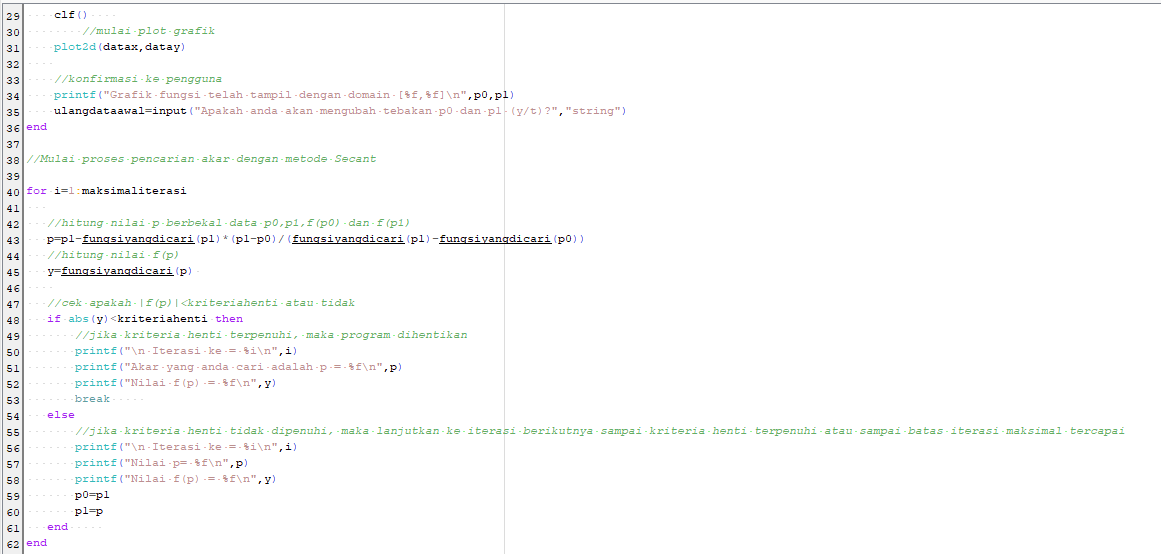
4. Metode Newton-Raphson

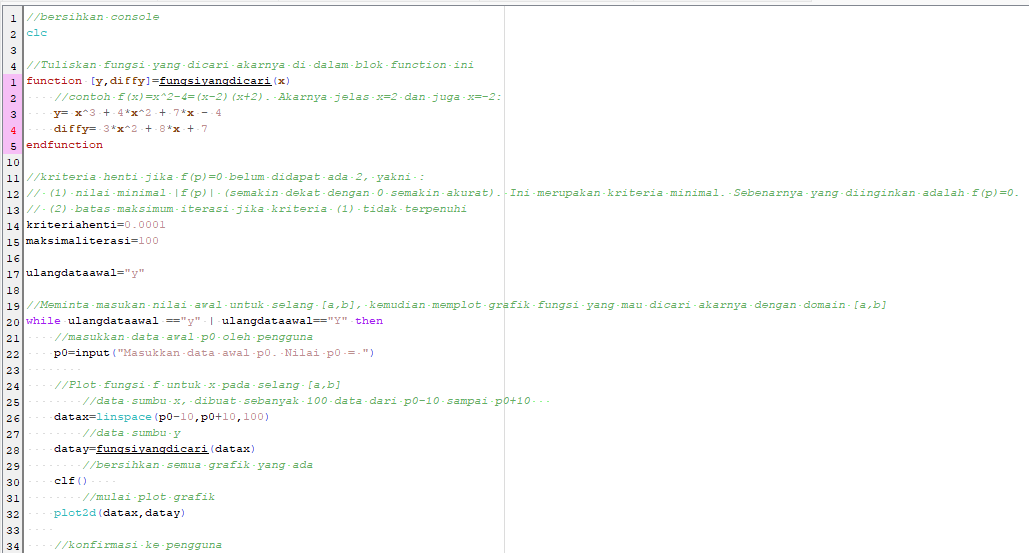
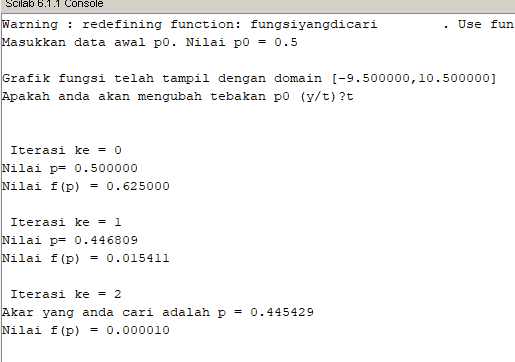
Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) memiliki turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

Langkah-langkah Metode Newton-Raphson:

1. Tentukan nilai awal x0

2. Hitung f(x0) kemudian cek konvergensi f(x0)

3. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Newton-Raphson :

 

 

 

 

Sekian uraian penjelasan langkah-langkah beserta syntax dari masing-masing metode pada sofwer scilab dalam pencarian akar persamaan tak linear. 

Semoga bermanfaat:)

Aamiin..