Penyelesaian Akar Persamaan Non-Linear dengan Metode Regulasi Falsi, Metode Iterasi Titik Tetap, Metode Newton-Raphson, Metode Secant Dengan Bantuan Aplikasi scilab
Dalam beberapa kasus, bentuk fungsi f (x) cukup kompleks sehingga tidak memungkinkan penentuan akar persamaan secara langsung. Sehingga dibutuhkan metode-metode yang dapat memecahkan masalah tersebut. Metode pencarian akar persamaan tak linear terderi atas dua metode, yaitu dengan metode tertutup dan metode terbuka. Metode tertutup terdiri atas Metode Bisection dan Metode Regulasi Falsi. Sedangkan metode terbuka terdiri atas Metode Iterasi Titik Tetap, Metode Newton-Raphson dan Metode Secant.
Berikut penyelesaian akar persamaan non-linear dengan metode regulasi falsi, metode iterasi titik tetap, metode Newton-Raphson dan metode secant dengan bantuan aplikasi scilab.
1. Metode Regulasi Falsi
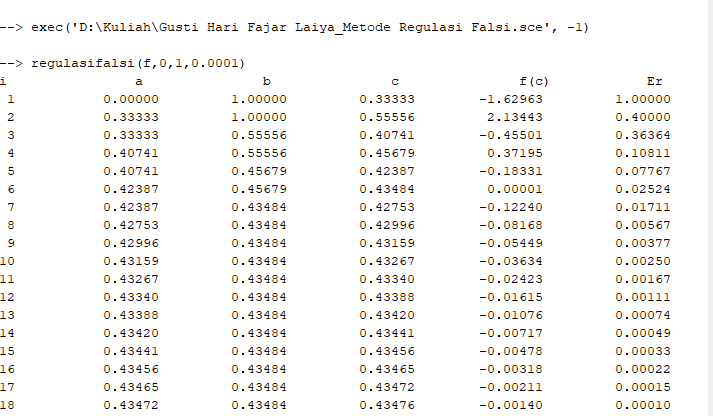
Berikut syntax scilab untuk metode Regulasi Falsi :

Hasil :

2. Metode Iterasi Titik Tetap
Berikut syntax scilab untuk metode Iterasi Titik Tetap :
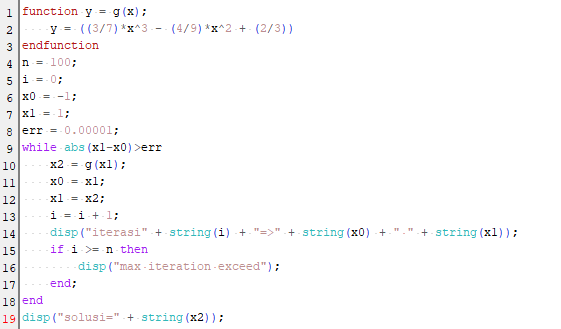
Hasil :

3. Metode Newton-Raphson
Berikut syntax scilab untuk metode Newton-Raphson :
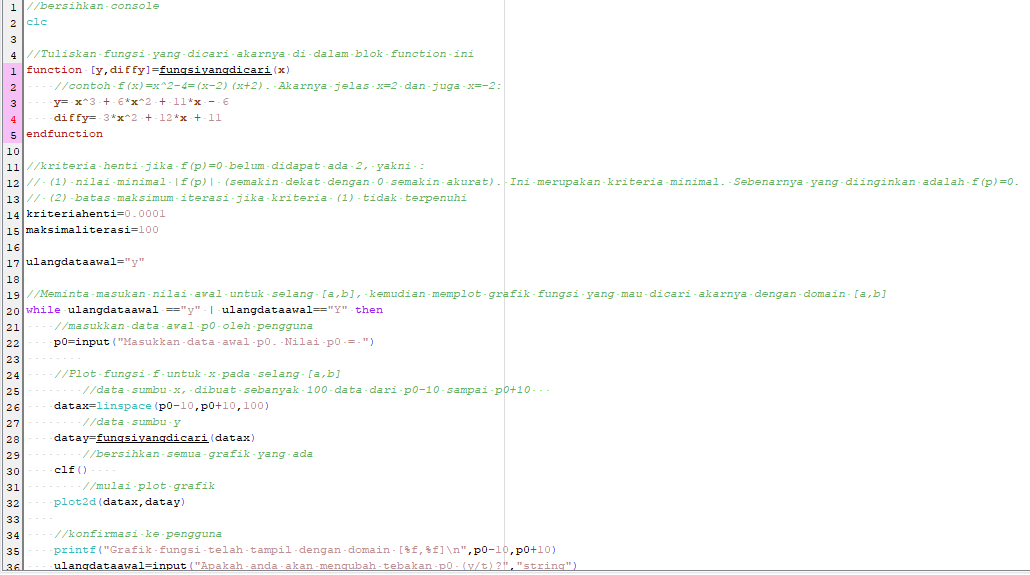
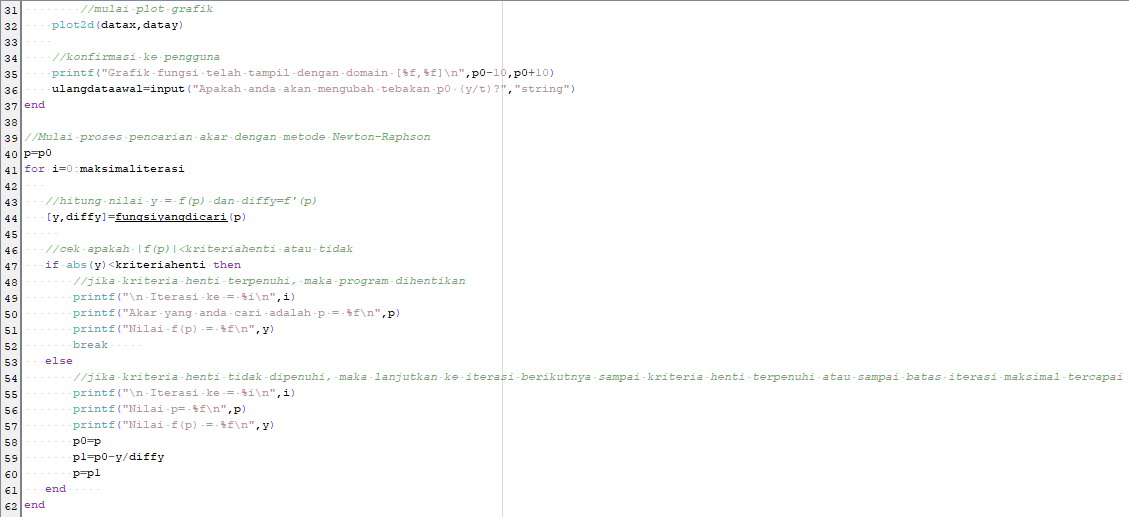
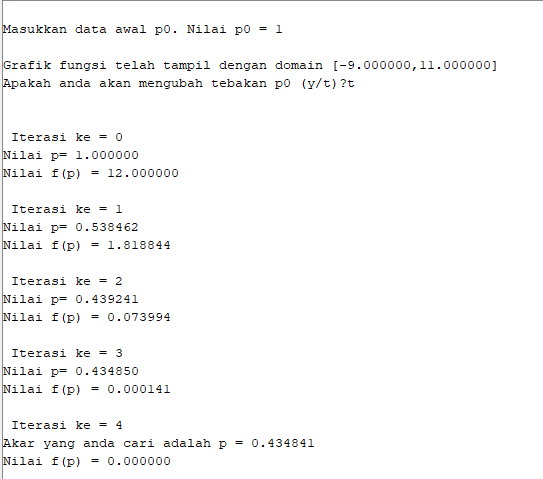
Hasil :
4. Metode Secant
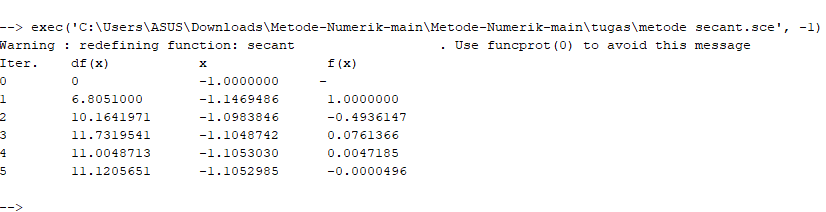
Berikut syntax scilab untuk metode Secant :
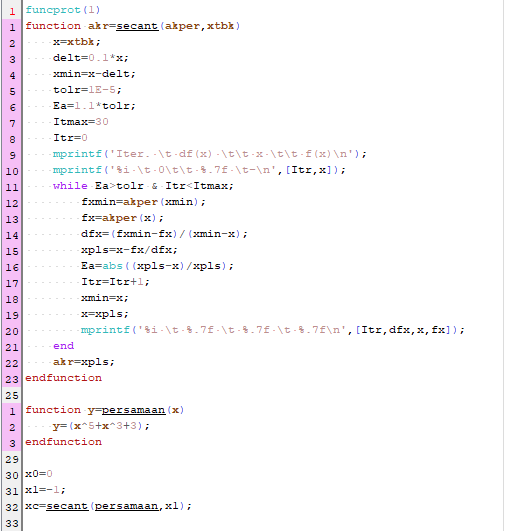
Hasil :