METODE NUMERIK

Metode Numerik merupakan suatu teknik yang digunakan untuk memformulasikan persoalan matematika sehinga dapat diselesaikan dengan menggunakan operasi aritmatika biasa. Pada umumnya metode numerik digunakan untuk menyelesaikan persoalan matematika yang tidak dapat diselesaikan dengan metode analitik biasa.Dalam Metode Numerik kita mengenal dua buah jenis sistem persamaan yaitu Sistem Persamaan Linier dan Sistem Persamaan Non-Linier. Masing-masing sistem persamaan memiliki beberapa metode. Dalam Sistem Persamaan Linier diantara metodenya adalah metode Eliminasi Gauss, metode Eliminasi Gauss-Jordan, metode Dekomposisi LU (Lower-Upper). Dan untuk Sistem Persamaan Non-Linier diantara metodenya adalah metode Bisection (Bagi-Dua), metode Regula Falsi, metode Newton Raphson, metode Secant, dan metode Fix Iteration. Pada kesempatan kali ini membahas tentang 2 buah metode yang ada dalam Sistem Persamaan Non-Linier, yaitu metode Titik Tetap dan metode Regula Falsi. Dan proses pembandingan ini menggunakan perangkat bahasa pemrograman scilab, hal ini untuk memudahkan dalam hal analisis algoritma penyelesaian metode, dan monitoring dalam hal waktu eksekusi dan analisis hasil output

Metode pencarian akar suatu persamaan dapat dilakukan dalam dua cara, yaitu melalui kekonvergenan secara global (metode tertutup) atau kekonvergenan lokal (metode terbuka). Metode yang pertama disebut juga metode pengapitan akar (bracket), oleh karena pencarian akar dilakukan pada suatu interval tertutup [a, b] sedemikian sehingga f(a) dan f(b) mempunyai tanda yang berlawanan. Metode ini terdiri atas:

Metode Bisection (Bagi Dua)Metode Regulasi Falsi (Posisi Palsu)Bila f(x) = 0 memiliki beberapa akar persamaan pada [a, b], maka interval awal yang berbeda harus digunakan untuk menemukan setiap akar persamaan tersebut.

Metode kekonvergenan lokal dalam menyelesaikan persamaan f(x) = 0 mensyaratkan suatu hampiran yang cukup dekat dengan akar persamaan sehingga menjamin kekonvergenan ke akar persamaan tersebut. Metode ini terdiri atas:

Metode Iterasi titik tetapMetode Newton-RaphsonMetode secantBila dibandingkan dengan metode kekonvergenan global, maka metode kekonvegenan lokal ini konvergen lebih cepat.

Berikut langkah-langkah beserta syntax pada aplikasi scilab dari masing-masing metode:

 

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dua titik batas jangkauan. Sebenarnya metode ini hampir sama dengan Metode Biseksi, namun titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi.

Langkah-langkah Metode Regulasi Falsi :

1. Tentukan nilai awal a dan b

2. Cek konvergensi nilai f(a) dan f(b)

Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnyaJika tanda f(a) = tanda f(b), pilih nilai awal yang baru3. Lakukan iterasi

4. Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))

5. Cek konvergensi nilai c

Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| Jika nilai Cn dan Cn-1 konstanJika nilai f(Cn) = 06. Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

Jika tanda f(c) = tanda f(a) maka c akan menggantikan aJika tanda f(c) = tanda f(b) maka c akan menggantikan b 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Regulasi Falsi :

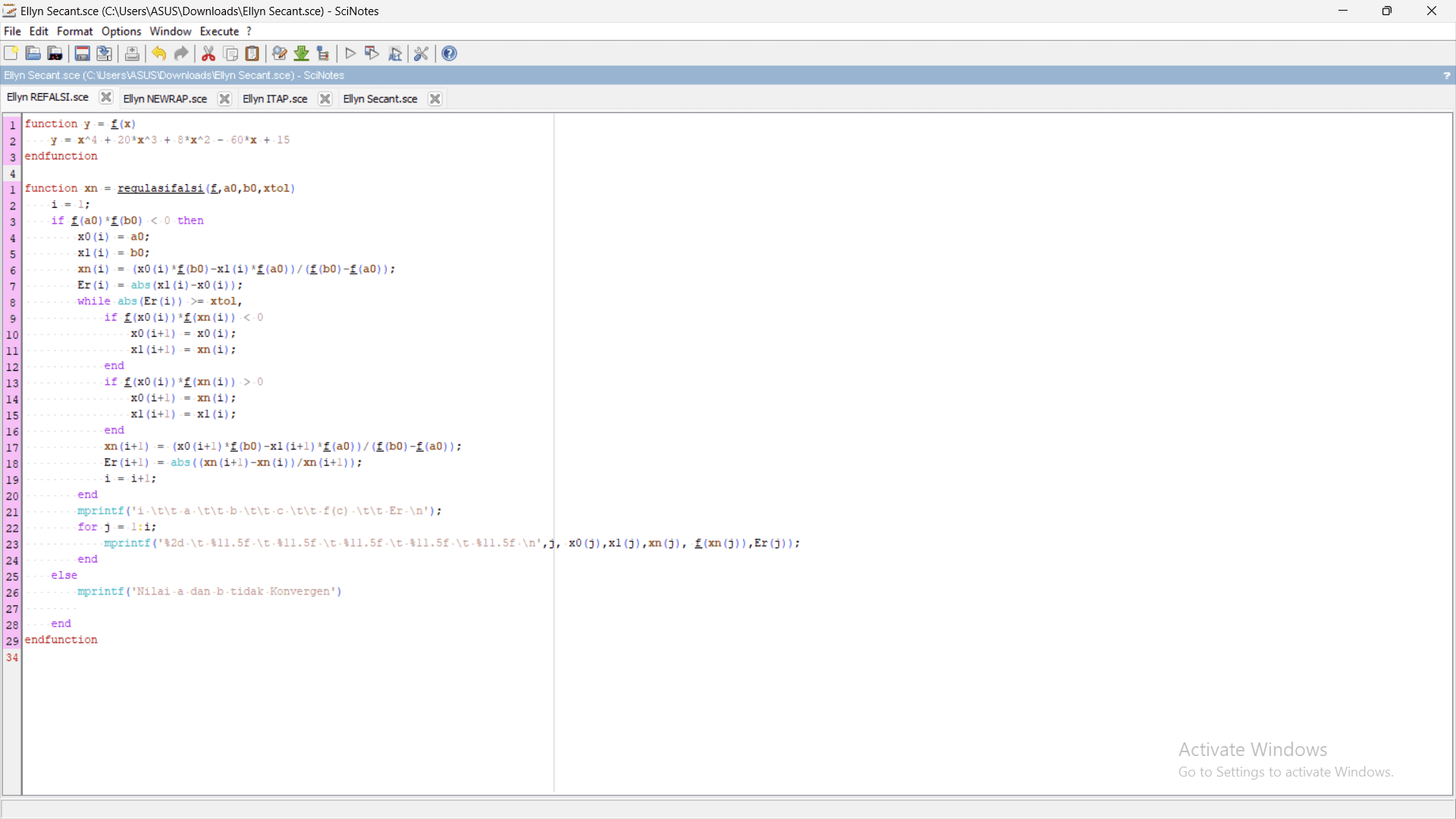
2. Metode Iterasi Titik Tetap

Metode iterasi titik tetap adalah suatu metode pencarian akar suatu fungsi f(x) secara sederhana dengan menggunakan satu titik awal. Metode iterasi titik tetap merupakan metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh x = g(x). Perlu diketahui bahwa fungsi f(x) yang ingin dicari hampiran akarnya harus konvergen. Misal x adalah Fixed Point (Titik Tetap) fungsi f(x) bila g(x) = x dan f(x) = 0.

Langkah-langkah Metode Iterasi Titik Tetap:

1. Susunlah persamaan f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:                             

                                                                    xn+1 = g(xn)

2. Tentukan nilai awal x0.

3. Lakukan iterasi dengan menghitung nilai x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

                                                        f (k) = 0 ; k = g(k)

4. Cek konvergensi terhadap XTOL (jika ada).

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Iterasi Titik Tetap :

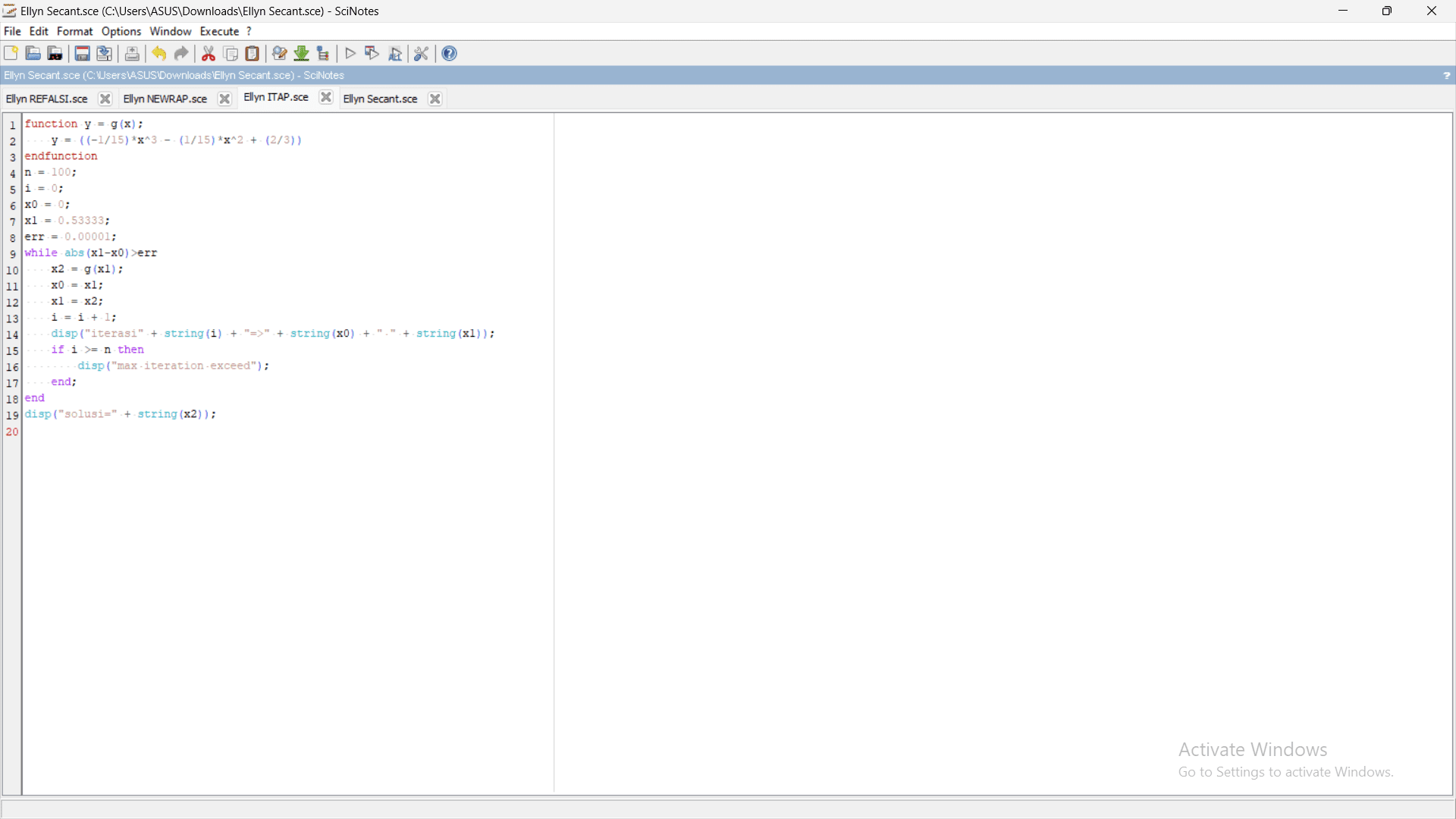
3. Metode Newton-Raphson

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) memiliki turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

Langkah-langkah Metode Newton-Raphson:

1. Tentukan nilai awal x0

2. Hitung f(x0) kemudian cek konvergensi f(x0)

3. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Newton-Raphson :

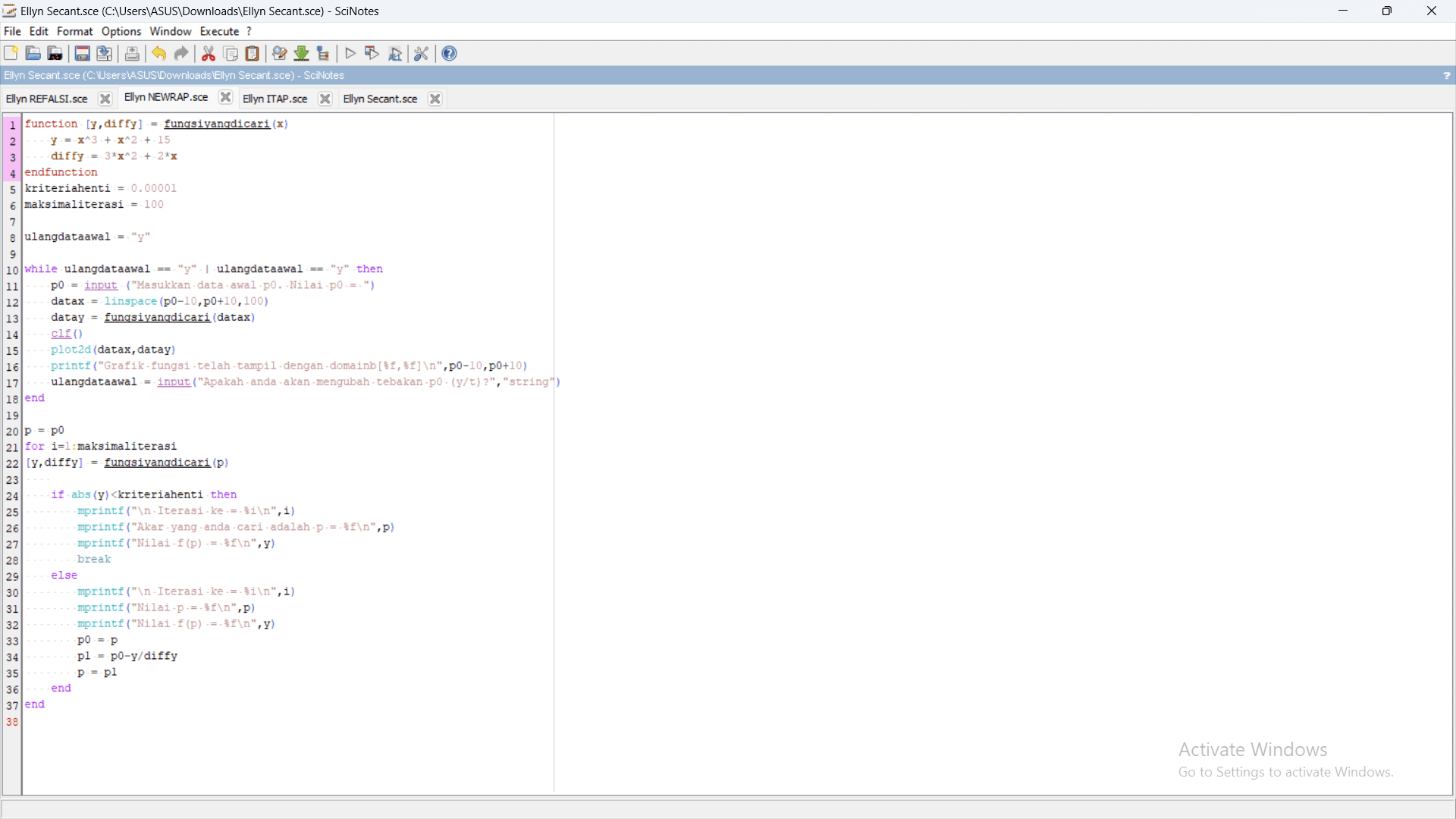
4. Metode Secant

Metode Secant merupakan metode modifikasi Newton-Raphson. Pada metode Newton-Raphson, pada setiap proses iterasinya memerlukan perhitungan nilai dua buah fungsi, yakni f(xn) dan f'(xn). Apabila kedua fungsi tersebut tidak rumit, metode tersebut mungkin sangat baik mengingat kekonvergenannya. Akan tetapi, tidak semua fungsi dapat diturunkan dengan mudah, terutama fungsi-fungsi yang rumit.Sedangkan metode Secant hanya memerlukan satu fungsi saja yaitu f(xn), yang jika pemrogramannya dilakukan dengan benar, maka akan diperoleh dari iterasi sebelumnya f(xn-1). Sehingga metode Secant akan memerlukan waktu yang lebih sedikit untuk tiap iterasinya dari pada Newton-Raphson.

Langkah-langkah Metode Secant:

1. Tentukan nilai awal x0 dan x1

2. Hitung f(x0) dan f(x1) kemudian cek konvergensi f(x0) dan f(x1)

3. Lakukan iterasi

4. Hitung nilai taksiran akar selanjutnya

           xn+1 = xn - f(xn) × (xn - xn-1)/(f(xn) - f(xn-1))

5. Cek konvergensi terhadap XTOL (Jika ada)

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Secant :

 

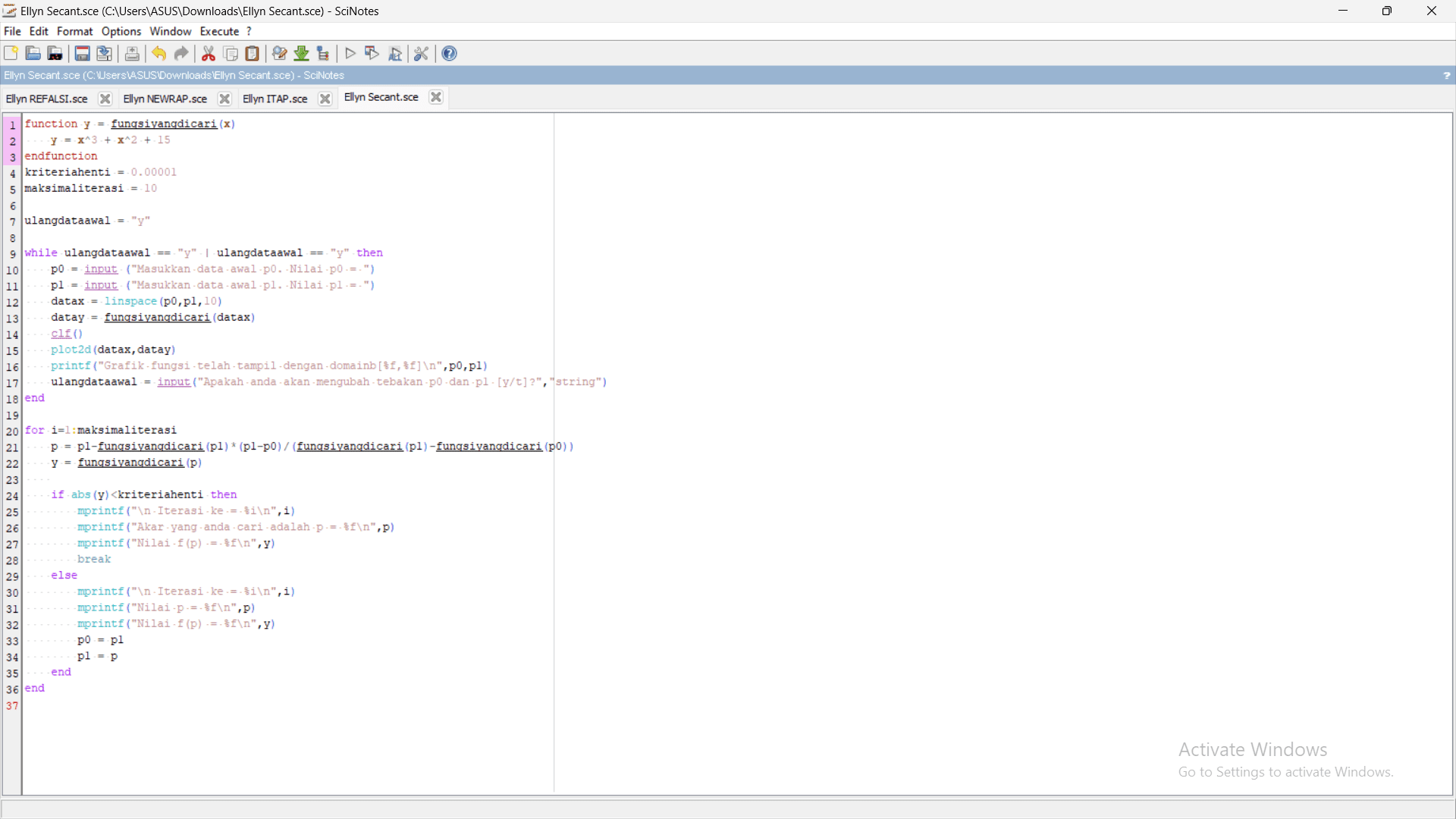
Demikian uraian penjelasan langkah-langkah beserta syntax dari masing-masing metode pada aplikasi scilab dalam pencarian akar persamaan tak linear. Lebih dan kurangnya saya mohon maaf.

Semoga bermanfaat:)