Metode numerik adalah teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan cara operasi hitungan. Dalam metode numerik ini dilakukan operasi hitungan dalam jumlah yang banyak dan prosesnya berulang. Sehingga dalam prakteknya perlu bantuan komputer untuk menyelesaikan hitungan tersebut. Tanpa bantuan komputer, metode numerik tidak banyak memberikan manfaat. Metode numerik merupakan alat yang sangat ampuh untuk menyelesaikan permasalahan dalam berbagai bidang. Metode numerik mampu menyelesaikan suatu sistim persamaan yang besar, persamaan yang tidak linier dan persamaan yang kompleks yang tidak mungkin diselesaikan secara analitis. 

Penyelesaian numerik dilakukan dengan iterasi, sehingga setiap hasil yang didapat selalu lebih teliti dibandingkan iterasi sebelumnya. Ada beberapa metode yang digunakan untuk menghitung akar-akar persamaan yaitu:

1. Metode Bisection
2. Metode Regula Falsi 
3. Metode Newton-Raphson
4. Metode Secant
5. Metode Iterasi Titik Tetap

Dalam kesempatan kali ini saya akan menunjukan perhitungan beberapa metode menggunaan aplikasi scilab.

Scilab adalah paket komputasi numerik lintas platform gratis dan open source serta bahasa pemrograman berorientasi numerik tingkat tinggi. Ini dapat digunakan untuk pemrosesan sinyal, analisis statistik, peningkatan citra, simulasi aliran, optimisasi dan pemodelan numerik, simulasi sistem dinamis eksplisit dan implisit, dan manipulasi simbolis.

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dari dua titik batas range. Sebenarnya metode ini hampir sama dengan Metode Biseksi, tapi titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi.

• Langkah-langkah Metode Regulasi Falsi

1. Tentukan nilai awal interval [a, b].
2. Cek konvergensi nilai f(a) dan f(b).
3. Lakukan iterasi dan tentukan nilai c (hitung akar)
4. Cek  konvergensi nilai c, jika nilai f(c) = 0 dan nilai cn+1 dan cn konstan, maka proses iterasi dihentikan.
5. Jika belum konvergen, tentukan nilai interval baru dengan cara:
• Jika tanda f(c) = tanda f(a) maka c = a  
• Jika tanda f(c) = tanda f(b) maka c = b

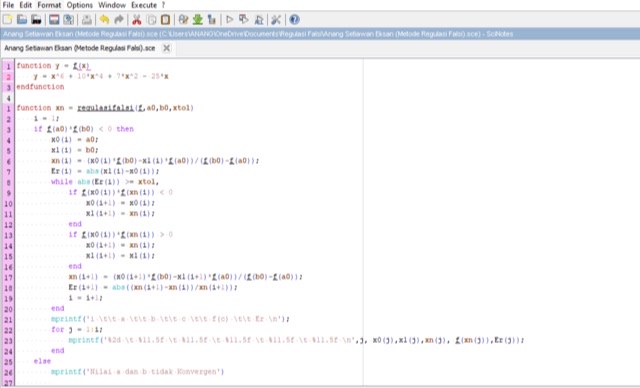
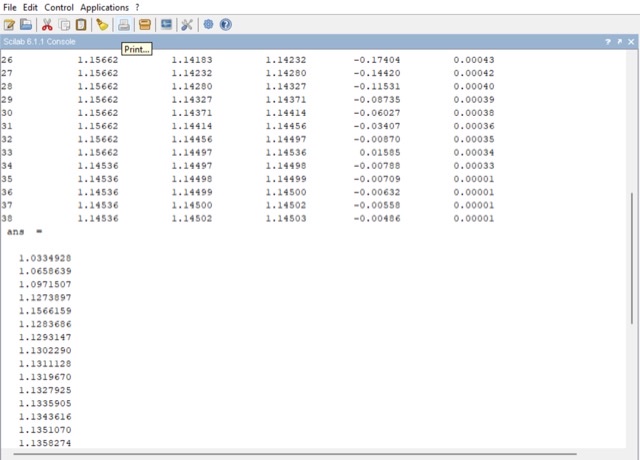
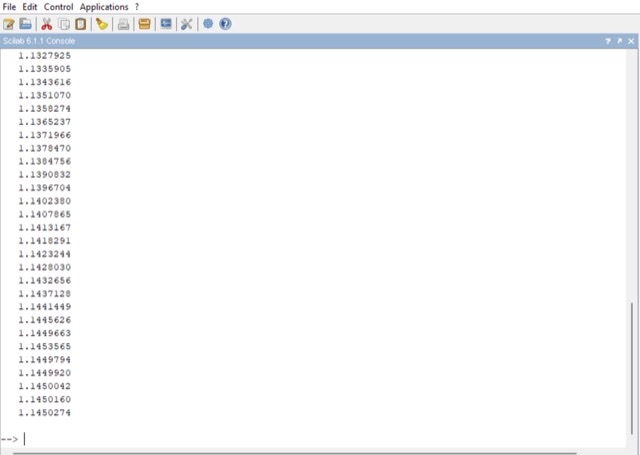
Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Regulasi Falsi :

2. Metode Iterasi Titip Tetap

Metode iterasi titik tetap merupakan metode penyelesaian persamaan non-linier dengan cara menyelesaikan setiap variabel xx yang ada dalam suatu persamaan dengan sebagian yang lain sehingga diperoleh x=g(x)x=g(x) untuk masing-masing variabel xx. Sebagai contoh, untuk menyelesaikan persamaan x+ex=0x+ex=0, maka persamaan tersebut perlu diubah menjadi x=exx=ex atau g(x)=exg(x)=ex.

• Langkah-langkah Metode Iterasi Titik Tetap

1. Ubah persamaan f(x) = 0 menjadi bentuk x = g(x)
2. Bentuk menjadi prosedur iterasi xn+1 = g(xn)
3. Tentukan sebuah nilai tawal x0
4. Hitung nilai x1,x2,x3,..., yang konvergen ke suatu titik s.

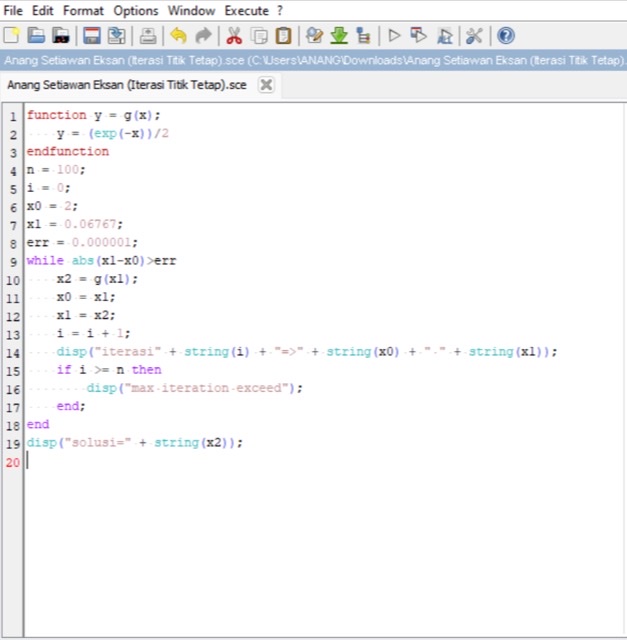
Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Iterasi Titik Tetapi :

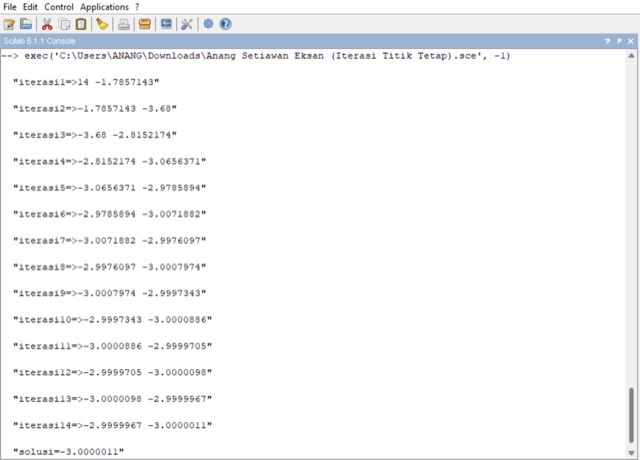
3. Metode Newton-Raphson

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

• Langkah-langkah Metode Newton-Raphson

1. Tentukan titik awal x0
2. Hitung f(x0) dan f'(x0)
3. Hitung xn = x0 - f(x0)/f'(x0) ; f'(x0)  0,n = 1,2,3,…
4. Iterasi lebih besar atau sama dengan iterasi maksimum tulis xhampiran = xn, jika tidak lanjut ke langkah selanjutnya.
5. Ganti nilai x0 = xn dan kembali ke langkah 4.

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Newton-Raphson :

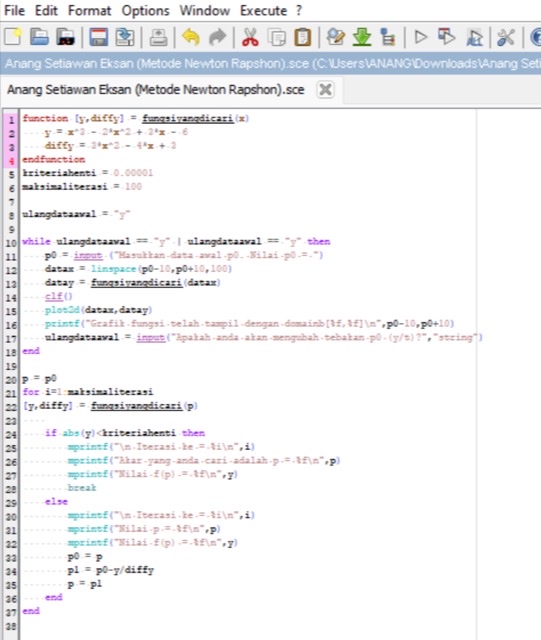
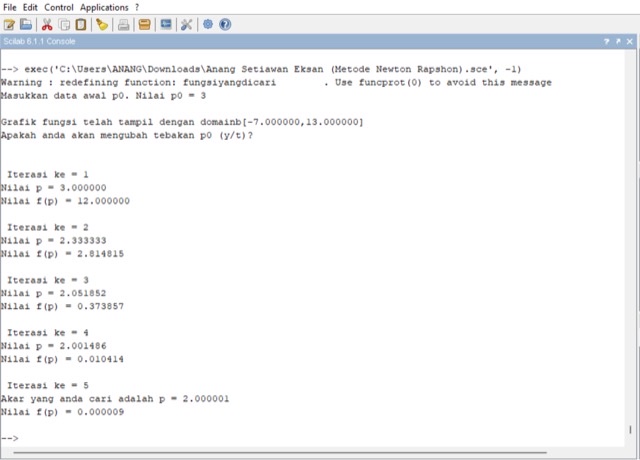
4. Metode Secant

Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f'(x). Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.

• Langkah-langkah Metode Secant

1. Tentukan x0, x1, toleransi, dan jumlah iterasi maksimum.
2. Hitung Xbaru = X1 - f(x1)( x1- x0)/f(x1) – f(x0).
3. Jika nilai mutlak (xbaru - x1) < toleransi, diperoleh tulisan xbaru sebagai hasil perhitungan.
4. Jika tidak, lanjutkan ke langkah berikutnya.
5. Jika jumlah iterasi > iterasi maksimum, akhiri program.
6. x = xbaru, dan kembali ke langkah (2).

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Secant :

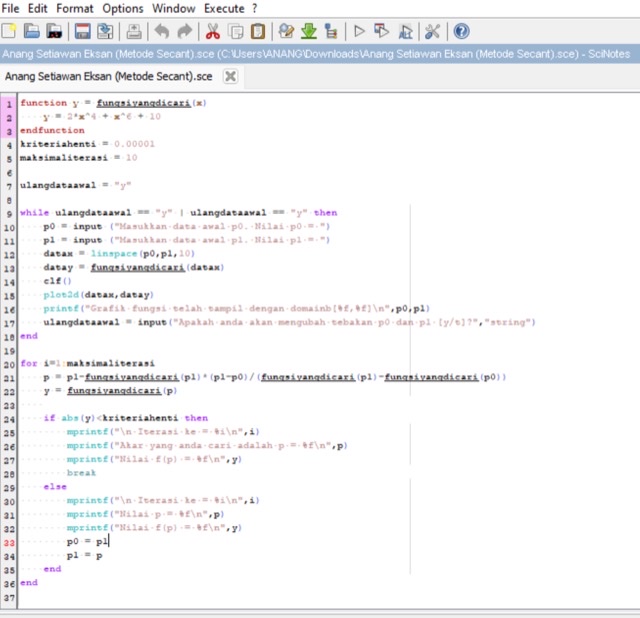
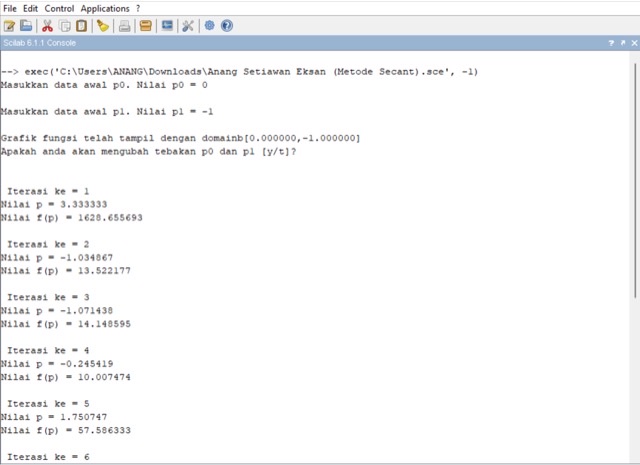
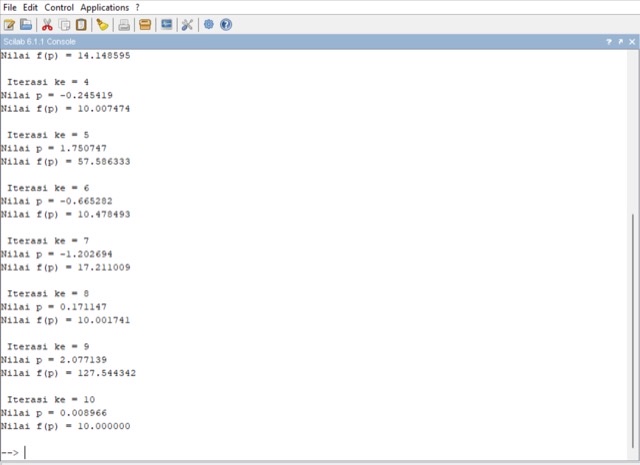
Demikian itulah beberapa uraian mengenai perhitungan menggunakan aplikasi scilab.

Arigatou gozaimasu...

Lomba Karya Tulis Ilmiah Nasional(LKTIN) adalah agenda tahunan yang diselenggarakan oleh IKAHIMATIKA Indonesia dan diikuti oleh perguruan tinggi-perguruan tinggi se-Indonesia. Di tahun 2021, omba Karya Tulis Ilmiah Nasional diselenggarakan di Universitas Sebelas Maret. Program Studi Matematika FMIPA UNG mengirimkan 5 tim untuk mengikuti ajang LKTIN tersebut yang dibimbing oleh bapak Resmawan, M.Si dan bapak Nisky Imansyah Yahya, M.Si.

Setelah melalui seleksi abstrak, kelima tim Matematika FMIPA UNG berhasil lolos ke tahap pemasukkan full paper. Kemudian, paper-paper yang masuk diseleksi kembali oleh panitia dan terpilih 18 tim untuk masuk ke dalam tahap final yaitu tahap presentasi. Tim Matematika FMIPA UNG berhasil mengirimkan 3 tim ke dalam tahap final ini.

Tim 1

Sunarwin Ismail

Melisa Huntala

Nurkalisa Laneto

Tim 2

Septi Rahmita Sari

Amelia Tri Rahma Sidik

Farhah Nadhilah

Tim 3

Sri Meylanti Ali

Haical Dunggio

Sri Ayu Nurdin 

Pada tahap final ini, masing-masing tim diberikan kesempatan untuk mempresentasikan ide karya tulis mereka dan setelah itu ada sesi tanya jawab dengan 3 orang juri LKTIN. Presentasi LKTIN IKAHIMATIKA Tahun 2021 berlangsung secara daring dari tanggal 25-26 Maret 2021. Setelah semua tim tampil mempresentasikan KTInya, tibalah dipenghujung kegiatan LKTIN yaitu pengumuman kejuaraan.

Alhamdulillah,salah satu tim Matematika FMIPA UNG yang diwakili oleh Septi Rahmita Sari (Matematika 2018), Amelia Tri Rahma Sidik (Matematika 2019) dan Farhah Nadhilah (Matematika 2020) berhasil meraih Juara 3 dalam Lomba Karya Tulis Nasional IKAHIMATIKA Indonesia Tahun 2021

Pemerintah Indonesia melalui Kementerian Pendidikan dan Kebudayaan kembali menyalurkan bantuan Kartu Indonesia Pintar – Kuliah (KIP-K) untuk para Calon Mahasiswa baru jalur SNMPTN dan SBMPTN tahun 2021.

Khusus jalur SNMPTN UNG dari 1.729 Calon Mahasiswa yang lulus, tercatat sebanyak 899 Calon Mahasiswa yang akan menikmati bantuan KIP-K dari Pemerintah selama mengikuti proses perkuliahan.

“UNG termasuk penerima terbanyak beasiswa KIP-K melalui jalur SNMPTN 2021,” ungkap Rektor UNG Dr. Ir. Eduart Wolok, S.T, M.T,.

Menurut Rektor dengan catatan 899 Calon Mahasiswa penerima KIP-K, secara Nasional UNG berada pada peringkat 5 Perguruan Tinggi yang banyak menerima beasiswa untuk Masyarakat kurang mampu tersebut.

“Beasiswa KIP-K disediakan khusus bagi Masyarakat kurang mampu tapi ingin melanjutkan pendidikan di Perguruan Tinggi. Syarat utama penerima beasiswa ini selain berstatus Masyarakat miskin tapi juga harus memiliki prestasi bidang akademik,”

Pengumuman hasil Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) untuk tahun 2021 telah resmi diumumkan oleh Lembaga Tes Masuk Perguruan Tinggi (LTMPT), tercatat ada 110.459 pendaftar yang dinyatakan lulus seleksi.

Untuk Calon Mahasiswa yang melakukan pendaftaran SNMPTN di Universitas Negeri Gorontalo, sebanyak 1.729 yang dinyatakan lulus dan berhak masuk UNG melalui seleksi jalur prestasi tersebut.

"Tahun ini pendaftar SNMPTN di UNG mencapai enam ribuan orang. Dari jumlah tersebut hanya 1.729 pendaftar saja yang dinyatakan lulus dan memenuhi standar penilaian oleh LTMPT untuk masuk ke UNG," ungkap Rektor UNG Dr. Ir. Eduart Wolok, S.T, M,T,.

Menurut Rektor, penentuan kelulusan SNMPTN ditentukan dari prestasi Calon Pendaftar selama duduk di bangku SMA/SMK/MA, yang dibuktikan dengan nilai raport di unggah melalui laman pendaftaran.

"Selamat kepada Calon Mahasiswa yang dinyatakan lulus SNMPTN di UNG. Kesempatan berharga tentunya harus dimanfaatkan sebaik-baiknya, karena tidak semua orang bisa lulus melalui jalur SNMPTN," terang Rektor.