Metode pencarian akar suatu persamaan dapat dilakukan dalam dua cara, yaitu melalui kekonvergenan secara global (metode tertutup) atau kekonvergenan lokal (metode terbuka). Metode yang pertama disebut juga metode pengapitan akar (bracket), oleh karena pencarian akar dilakukan pada suatu interval tertutup [a, b] sedemikian sehingga  dan  mempunyai tanda yang berlawanan. Metode ini terdiri atas:

• Metode Bisection (Bagi Dua)
• Metode Regulasi Falsi (Posisi Palsu)

Bila  memiliki beberapa akar persamaan pada [a, b], maka interval awal yang berbeda harus digunakan untuk menemukan setiap akar persamaan tersebut.

Metode kekonvergenan lokal dalam menyelesaikan persamaan mensyaratkan suatu hampiran yang cukup dekat dengan akar persamaan sehingga menjamin kekonvergenan ke akar persamaan tersebut. Metode ini terdiri atas:

• Metode Iterasi titik tetap
• Metode Newton-Raphson
• Metode secant

Bila dibandingkan dengan metode kekonvergenan global, maka metode kekonvegenan lokal ini konvergen lebih cepat. Berikut langkah-langkah beserta syntax pada aplikasi scilab dari masing-masing metode:

METODE REGULASI FALSI

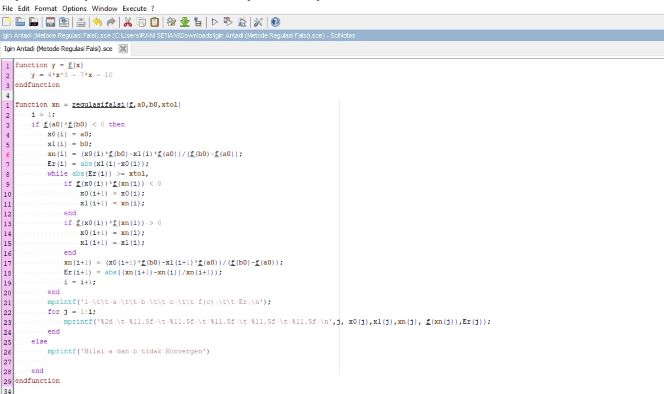
Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dari dua titik batas range. 

Rumus : C=(f(b).a-f(a).b)/(f(b)-f(a))

 Langkah-langkah regulasi falsi

1. Tentukan nilai awal interval [a, b].
2. Cek konvergensi nilai f(a) dan f(b).
3. Lakukan iterasi dan tentukan nilai c (hitung akar)
4. Cek konvergensi nilai c, jika nilai f(c) = 0 dan nilai cn+1 dan cn konstan, maka proses iterasi dihentikan.
5. Jika belum konvergen, tentukan nilai interval baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c = a
• Jika tanda f(c) = tanda f(b) maka c = b

Berikut syntax scilab untuk metode Regulasi Falsi :

 

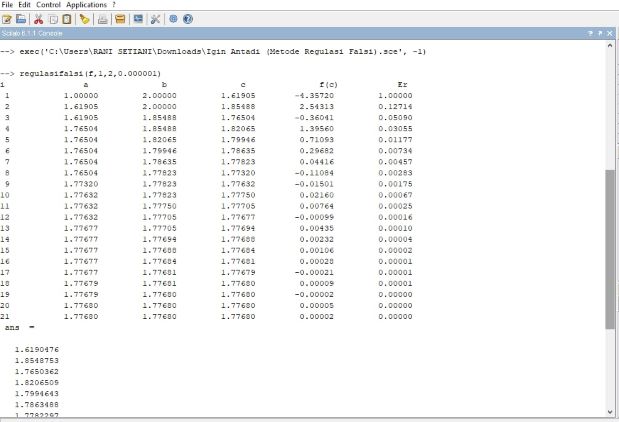
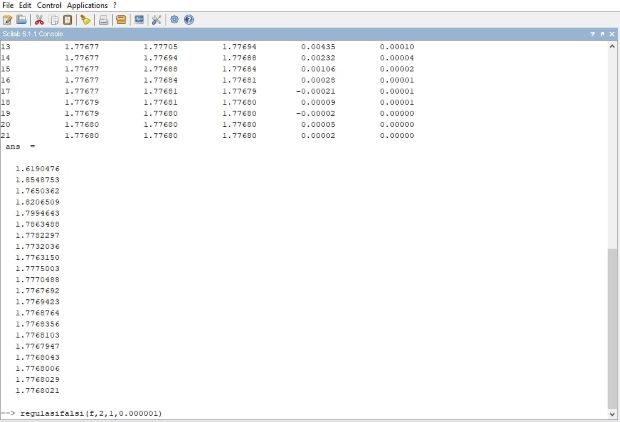
Hasil :

 

 

 

 

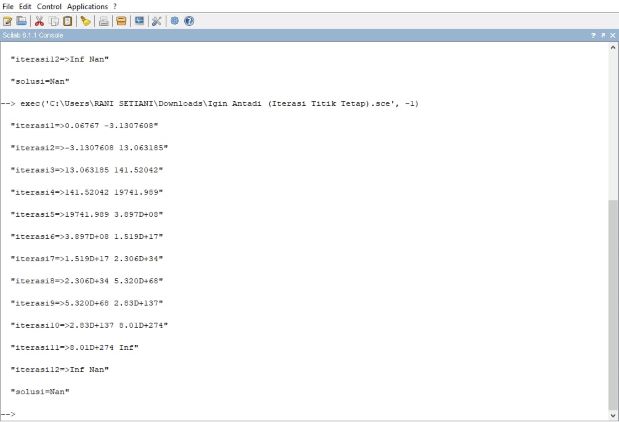
METODE ITERASI TITIK TETAP

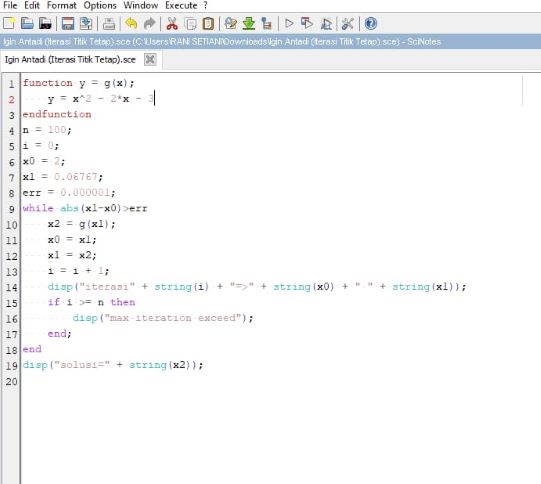
Metode iterasi titik tetap adalah suatu metode pencarian akar suatu fungsi f(x) secara sederhana dengan menggunakan satu titik awal. Metode iterasi titik tetap merupakan metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh x = g(x). Perlu diketahui bahwa fungsi f(x) yang ingin dicari hampiran akarnya harus konvergen. Misal x adalah Fixed Point (Titik Tetap) fungsi f(x) bila g(x) = x dan f(x) = 0.

Langkah-langkah Metode Iterasi Titik Tetap:

1. Susunlah persamaan f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:

xn+1 = g(xn)

2. Tentukan nilai awal x0.

3. Lakukan iterasi dengan menghitung nilai x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

f (k) = 0 ; k = g(k)

4. Cek konvergensi terhadap XTOL (jika ada).

Berikut syntax scilab untuk metode Iterasi Titik Tetap:

 

Hasil :

 

 

METODE NEWTON RAPSHON

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) memiliki turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

Langkah-langkah Metode Newton-Raphson:

1. Tentukan nilai awal x0

2. Hitung f(x0) kemudian cek konvergensi f(x0)

3. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

Berikut syntax scilab untuk metode Newton-Raphson:

 

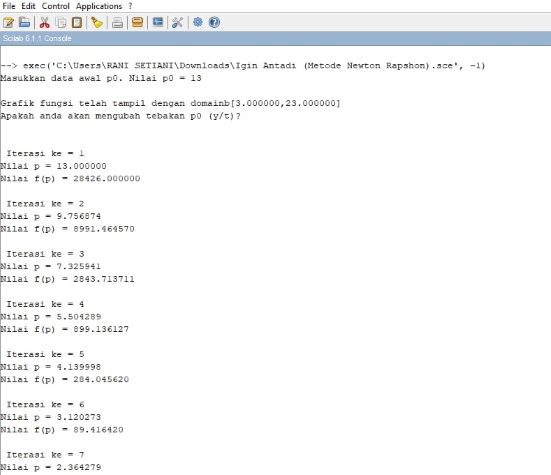
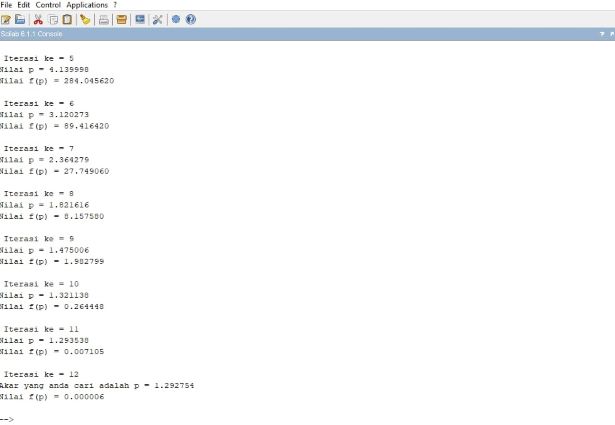
Hasil ;

 

 

 

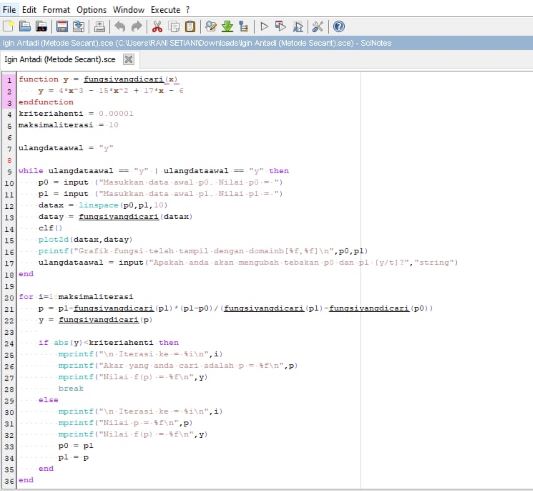
METODE SECANT

Metode Secant merupakan metode modifikasi Newton-Raphson. Pada metode Newton-Raphson, pada setiap proses iterasinya memerlukan perhitungan nilai dua buah fungsi, yakni f(xn) dan f'(xn). Apabila kedua fungsi tersebut tidak rumit, metode tersebut mungkin sangat baik mengingat kekonvergenannya. Akan tetapi, tidak semua fungsi dapat diturunkan dengan mudah, terutama fungsi-fungsi yang rumit.Sedangkan metode Secant hanya memerlukan satu fungsi saja yaitu f(xn), yang jika pemrogramannya dilakukan dengan benar, maka akan diperoleh dari iterasi sebelumnya f(xn-1). Sehingga metode Secant akan memerlukan waktu yang lebih sedikit untuk tiap iterasinya dari pada Newton-Raphson.

Langkah-langkah Metode Secant:

1. Tentukan nilai awal x0 dan x1

2. Hitung f(x0) dan f(x1) kemudian cek konvergensi f(x0) dan f(x1)

3. Lakukan iterasi

4. Hitung nilai taksiran akar selanjutnya

xn+1 = xn - f(xn) × (xn - xn-1)/(f(xn) - f(xn-1))

5. Cek konvergensi terhadap XTOL (Jika ada)

Berikut syntax scilab untuk metode Secant:

 

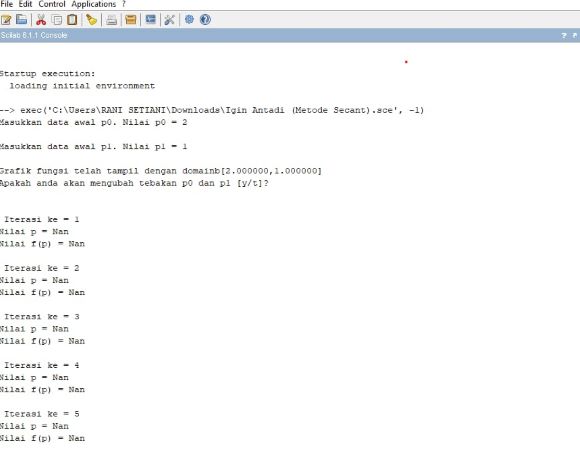
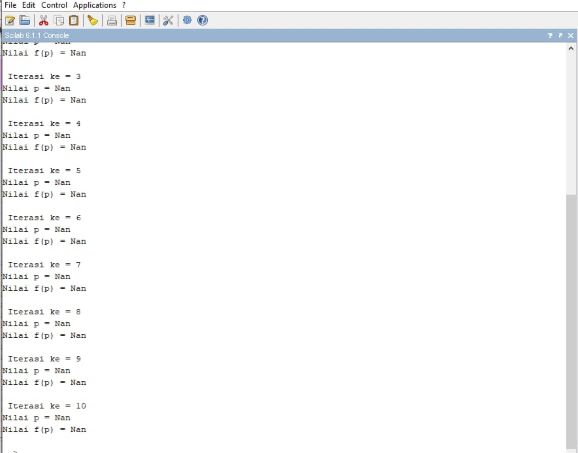
Hasil :

 

 

Pendidikan sangat penting bagi semua orang yang bertujuan untuk mencerdaskan dan mengembangkan potensi dalam diri. Dengan semakin bertumbuh dan berkembang setiap orang bisa memiliki kreativitas, pengetahuan yang lebih luas, kepribadian yang baik dan menjadi pribadi yang bertanggung jawab.

Namun, jika kita sudah berpendidikan, janganlah kita memandang orang yang tidak berpendidikan itu seakan-akan mereka rendah. Tapi, kita harus menunjukan bahwa orang yang berpendidikan itu adalah orang yang bisa menghargai sesama manusia.

Tidak bisa di pungkiri bahwa perguruan tinggi atau universitas merupakan salah satu jembatan yang menghubungkan seseorang dengan kesuksesan.

Tapi, alasan saya masuk di Universitas Negeri Gorontalo yakni, UNG telah menghasilkan lulusan atau alumni yang begitu banyak, dan telah di terima diberbagai bidang pekerjaan. Selain itu, kampus UNG juga memiliki fasilitas yang memadai, aman, bersih, religi, dan bebas narkoba, sehingga membuat saya yakin untuk menimbah ilmu di Universitas Negeri Gorontalo (UNG).

Berhenti berpikir bahwa matematika itu terlalu abstrak untuk dipelajari.

Dan pastikan juga kamu yakin bahwa matematika itu tidak se-abstrak seperti yang orang-orang bilang bahwa, "matematika banyak rumusnya lah atau matematika itu dosennya killer-killer!", 'Buat apa kamu ngambil jurusan matematika, toh integral gak akan kamu temui dalam kehidupan sehari-hari!"

Wop...salah banget nih guys. Buat kamu yang mau masuk jurusan matematika, kamu perlu tau apa saja manfaat mengambil jurusan matematika.

Manfaat mengambil jurusan matematika adalah:

1. Matematika ada di hampir setiap hari dalam hidupmu 
2. Matematika melatihmu menjadi orang yang kritis, analistis,dan disiplin
3. Algoritma dalam matematika melatihmu dapat mengambil keputusan dengan tepat dalam persoalan sehari-hari
4. Matematika melatihmu menjadi orang yang sabar dan pantang menyerah
5. Matematika memiliki prospek kerja yang luas