Metode pencarian akar suatu persamaan dapat dilakukan dalam dua cara, yaitu melalui kekonvergenan secara global (metode tertutup) atau kekonvergenan lokal (metode terbuka). Metode yang pertama disebut juga metode pengapitan akar (bracket), oleh karena pencarian akar dilakukan pada suatu interval tertutup [a, b] sedemikian sehingga f(a) dan f(b) mempunyai tanda yang berlawanan. Metode ini terdiri atas:

• Metode Bisection (Bagi Dua)
• Metode Regulasi Falsi (Posisi Palsu)

Bila f(x) = 0 memiliki beberapa akar persamaan pada [a, b], maka interval awal yang berbeda harus digunakan untuk menemukan setiap akar persamaan tersebut.

Metode kekonvergenan lokal dalam menyelesaikan persamaan f(x) = 0 mensyaratkan suatu hampiran yang cukup dekat dengan akar persamaan sehingga menjamin kekonvergenan ke akar persamaan tersebut. Metode ini terdiri atas:

• Metode Iterasi titik tetap
• Metode Newton-Raphson
• Metode secant

Bila dibandingkan dengan metode kekonvergenan global, maka metode kekonvegenan lokal ini konvergen lebih cepat.

Berikut langkah-langkah beserta syntax pada aplikasi scilab dari masing-masing metode:

 

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dua titik batas jangkauan. Sebenarnya metode ini hampir sama dengan Metode Biseksi, namun titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi.

Langkah-langkah Metode Regulasi Falsi :

1. Tentukan nilai awal a dan b

2. Cek konvergensi nilai f(a) dan f(b)

• Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnya
• Jika tanda f(a) = tanda f(b), pilih nilai awal yang baru

3. Lakukan iterasi

4. Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))

5. Cek konvergensi nilai c

• Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| 
• Jika nilai Cn dan Cn-1 konstan
• Jika nilai f(Cn) = 0

6. Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c akan menggantikan a
• Jika tanda f(c) = tanda f(b) maka c akan menggantikan b

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Regulasi Falsi :

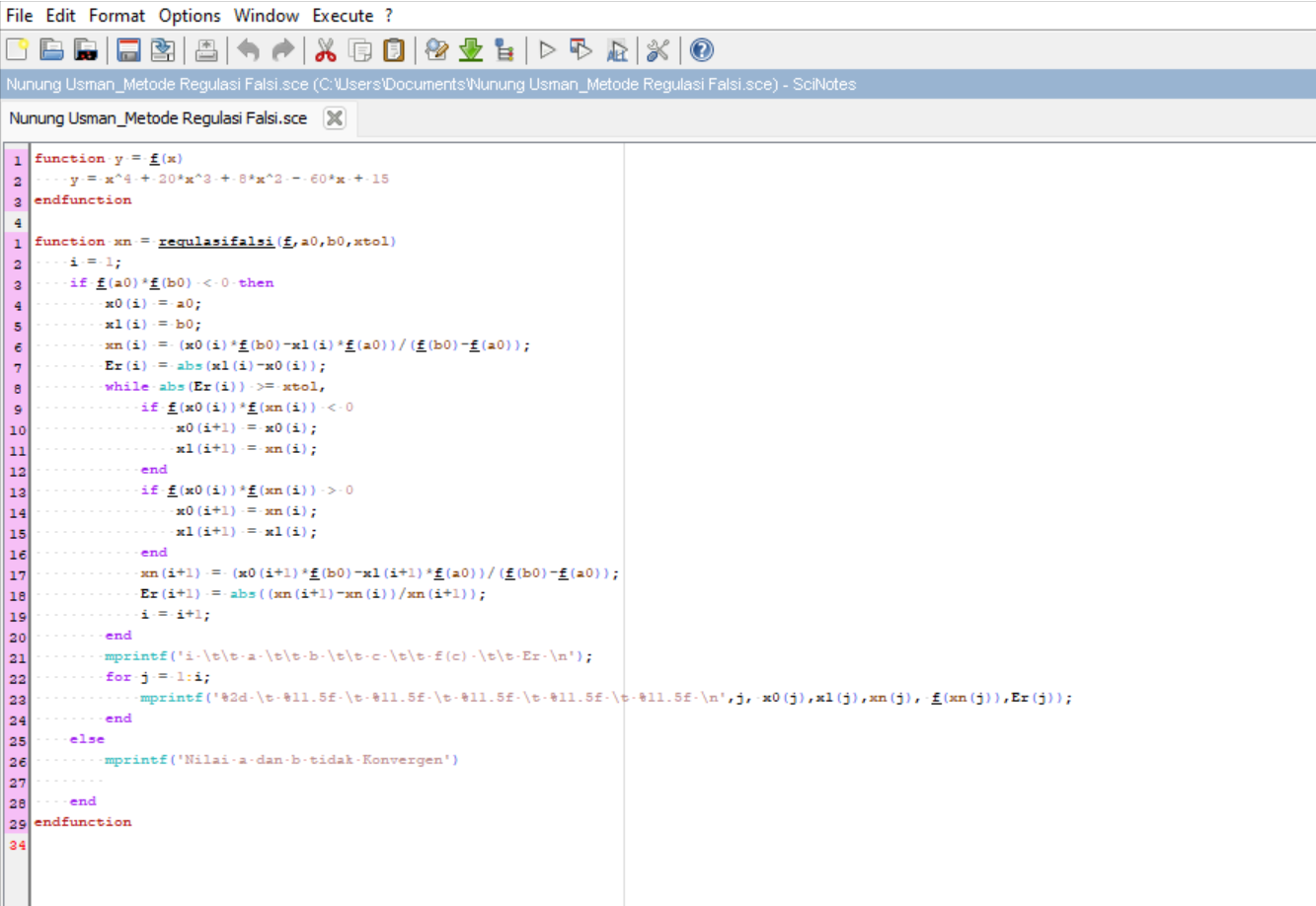
Hasil :

 

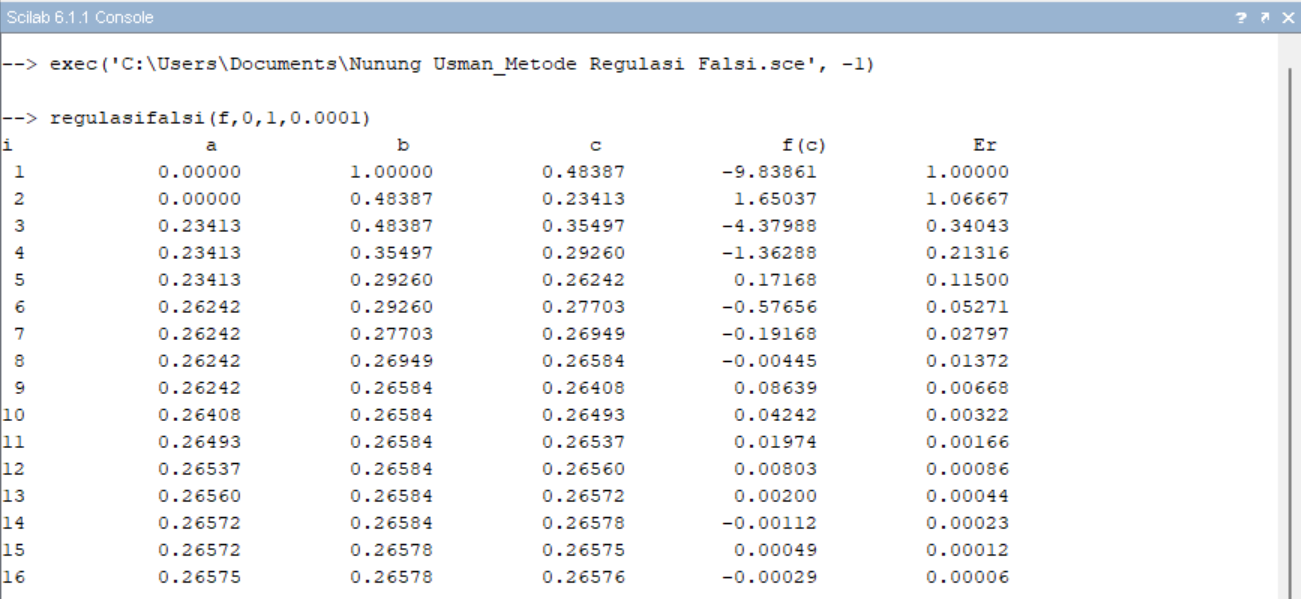
2. Metode Iterasi Titik Tetap

Metode iterasi titik tetap adalah suatu metode pencarian akar suatu fungsi f(x) secara sederhana dengan menggunakan satu titik awal. Metode iterasi titik tetap merupakan metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh x = g(x). Perlu diketahui bahwa fungsi f(x) yang ingin dicari hampiran akarnya harus konvergen. Misal x adalah Fixed Point (Titik Tetap) fungsi f(x) bila g(x) = x dan f(x) = 0.

Langkah-langkah Metode Iterasi Titik Tetap:

1. Susunlah persamaan f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:                             

                                                                    xn+1 = g(xn)

2. Tentukan nilai awal x0.

3. Lakukan iterasi dengan menghitung nilai x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

                                                        f (k) = 0 ; k = g(k)

4. Cek konvergensi terhadap XTOL (jika ada).

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Iterasi Titik Tetap :

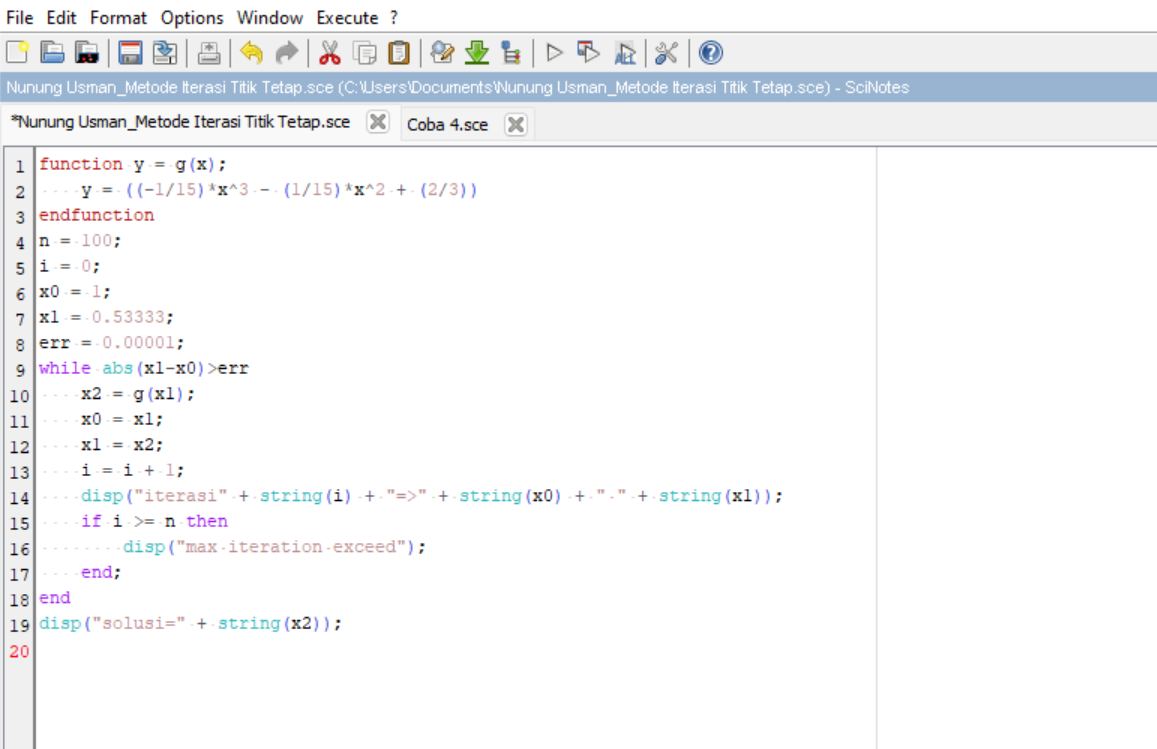
Hasil :

 

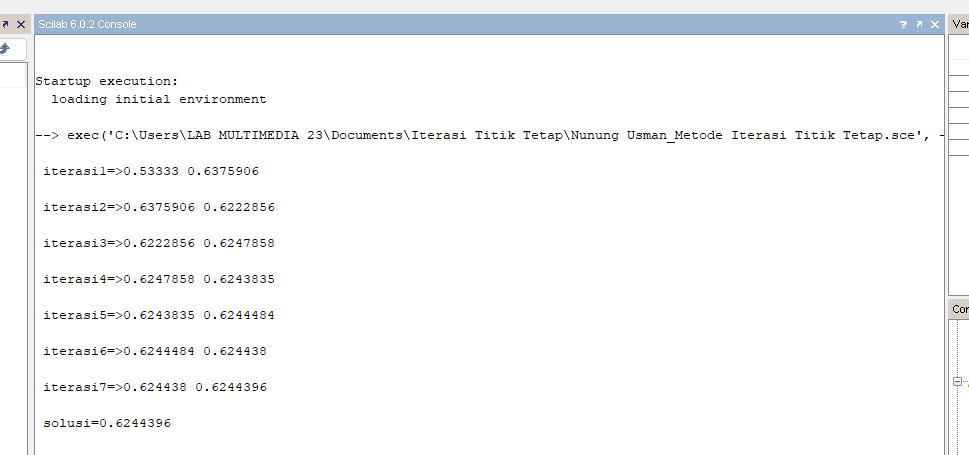
3. Metode Newton-Raphson

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) memiliki turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

Langkah-langkah Metode Newton-Raphson:

1. Tentukan nilai awal x0

2. Hitung f(x0) kemudian cek konvergensi f(x0)

3. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Newton-Raphson :

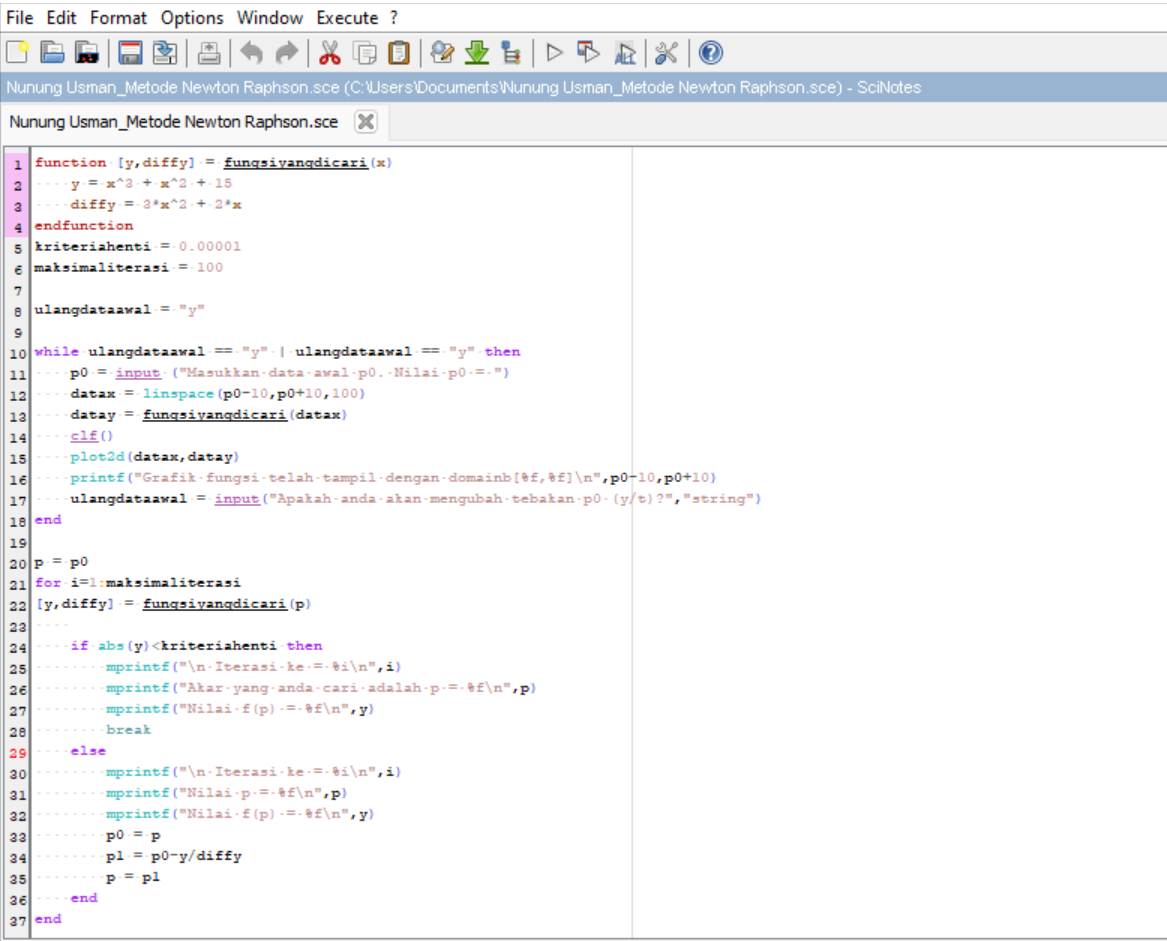
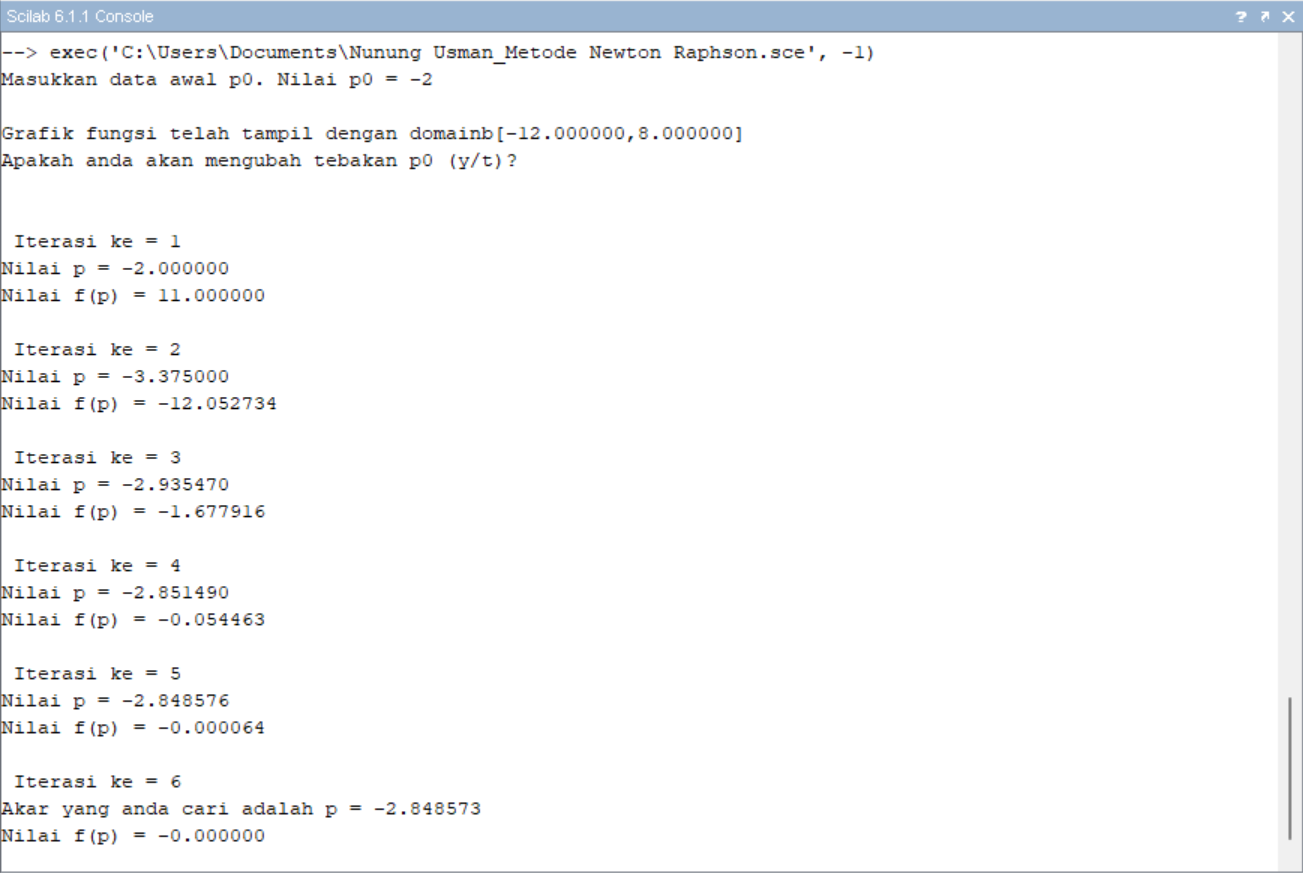
Hasil :

 

4. Metode Secant

Metode Secant merupakan metode modifikasi Newton-Raphson. Pada metode Newton-Raphson, pada setiap proses iterasinya memerlukan perhitungan nilai dua buah fungsi, yakni f(xn) dan f'(xn). Apabila kedua fungsi tersebut tidak rumit, metode tersebut mungkin sangat baik mengingat kekonvergenannya. Akan tetapi, tidak semua fungsi dapat diturunkan dengan mudah, terutama fungsi-fungsi yang rumit.Sedangkan metode Secant hanya memerlukan satu fungsi saja yaitu f(xn), yang jika pemrogramannya dilakukan dengan benar, maka akan diperoleh dari iterasi sebelumnya f(xn-1). Sehingga metode Secant akan memerlukan waktu yang lebih sedikit untuk tiap iterasinya dari pada Newton-Raphson.

Langkah-langkah Metode Secant:

1. Tentukan nilai awal x0 dan x1

2. Hitung f(x0) dan f(x1) kemudian cek konvergensi f(x0) dan f(x1)

3. Lakukan iterasi

4. Hitung nilai taksiran akar selanjutnya

           xn+1 = xn - f(xn) × (xn - xn-1)/(f(xn) - f(xn-1))

5. Cek konvergensi terhadap XTOL (Jika ada)

 

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax scilab untuk metode Secant :

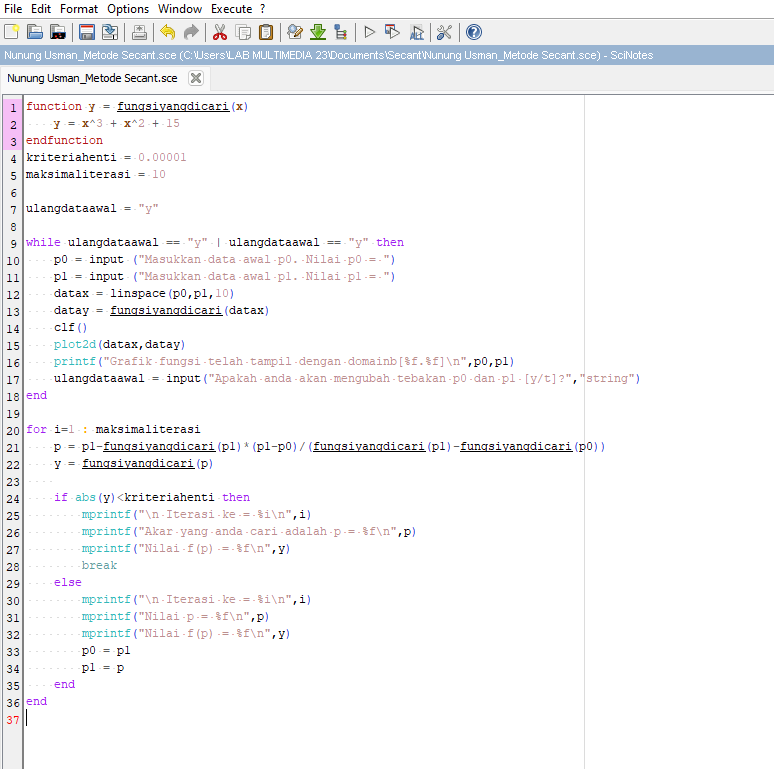
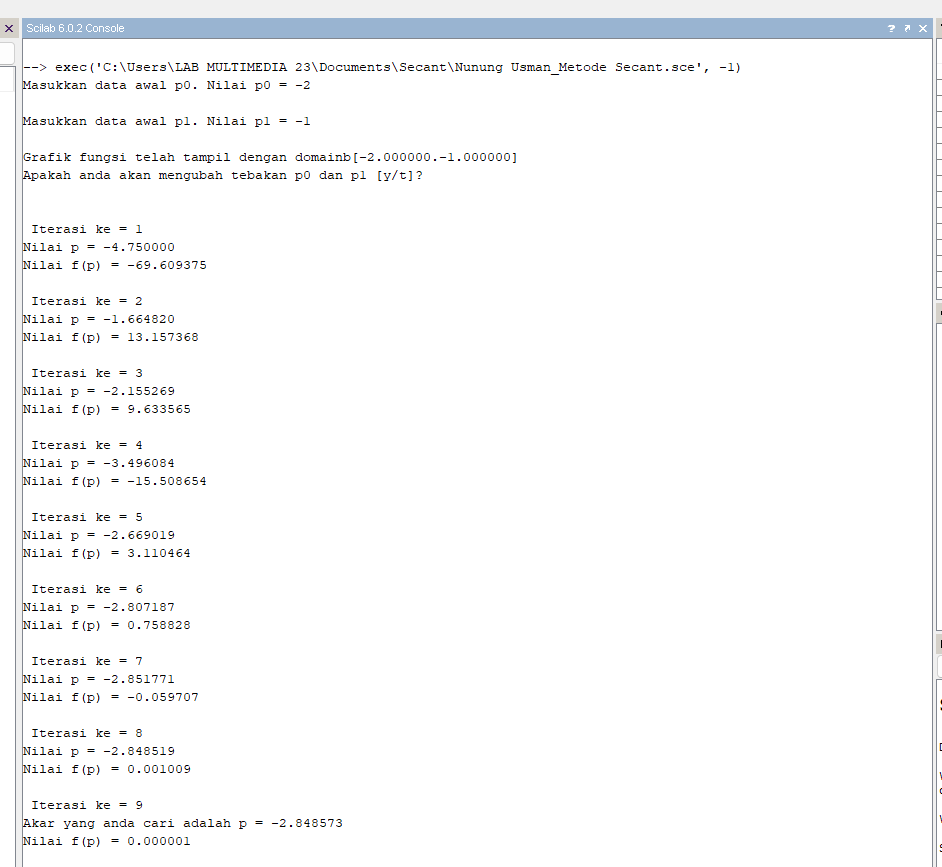
Hasil :

 

Demikian uraian penjelasan langkah-langkah beserta syntax dari masing-masing metode pada aplikasi scilab dalam pencarian akar persamaan tak linear. Lebih dan kurangnya saya mohon maaf.

Semoga bermanfaat:)

Organisasi mahasiswa di kampus merupakan sebuah wadah berprosesnya seorang mahasiswa, berproses melalui pemikiran serta tindakan. Di organisasi seorang mahasiswa dapat mengetahui tata cara berbicara yang baik dalam forum, mengasah mental ketika berada di tengah forum, dan belajar musyawarah dalam sebuah jejak pendapat untuk menghasilkan ataupun memutuskan sesuatu.

Di organisasi mahasiswa kita benar-benar merasakan bagaimana bertanggung jawab sesuai amanah dan tugas yang kita emban untuk melaksanakannya dengan baik, terlebih juga dalam organisasi mahasiswa kita dapat mempraktekan ilmu yang kita dapatkan selama berproses didalamnya.

Di organisasi mahasiswalah kita dapat pembelajaran ilmu-ilmu yang membuat kita peka terhadap sesama, membuat kita lebih percaya diri, membuat kita lebih tenang ketika menghadapi masalah, serta sebagai miniatur tempat kita berkontribusi dalam pemikiran serta tindakan.

Dalam organisasilah juga kita belajar apa itu Team Work, bagaimana memerintah dan diperintah. Karena apabila kita ingin menjadi seorang pemimpin maka kita juga harus siap dipimpin. Dengan berorganisasilah kita memiliki bekal untuk kehidupan di masa yang akan datang.

Penghargaan diberikan pihak Universitas Negeri Gorontalo (UNG) kepada sejumlah mahasiswa yang telah mengharumkan nama UNG di tingkat nasional. Penghargaan ini diberikan dalam acara Malam Anugerah Prestasi Kemahasiswaan dan Alumni tahun 2020, yang digelar Kamis (3/8).

Tidak hanya mahasiswa, penghargaan juga diberikan kepada para pegawai dan tenaga kependidikan yang berhasil menoreh prestasi.

Adapun beberapa prestasi yang di apresiasi di antaranya, Program Kreatifitas Mahasiswa yang berhasil lolos hibah Kementerian, Pemenang Hibah PHP2D, Program Holistik Pembinaan dan Pemberdayaan Desa tahun 2020, serta Kelompok hibah Kompetisi Bisnis Manajemen Mahasiswa Indonesia (KBMI) yang lolos seleksi hibah tahun 2020.

Penghargaan juga diberikan kepada mahasiswa yang membawa nama baik UNG khusus bidang akademik maupun non akademik baik ditingkat regional serta Nasional, Kelompok Mahasiswa KKS perintis Desa Inovasi Dusun Tumba Desa Tamaila Utara.

Rektor UNG, Dr. Eduart Wolok mengungkapkan, dalam kurun waktu satu tahun ini banyak prestasi yang ditoreh UNG sehingga menjadi satu kebanggaan bersama bagi Gorontalo.

Pencapaian bidang kemahasiswaan menurut Eduart sangatlah membanggakan, yang dibuktikan dengan banyaknya prestasi yang dicatatkan dalam kurun waktu satu tahun.

Universitas Negeri Gorontalo atau yang disingkat UNG merupakan perguruan tinggi negeri (PTN) di Gorontalo yang berdiri pada 1 September 1963.

Keberadaan Universitas Negeri Gorontalo dimulai dari Junior College FKIP Universitas Sulawesi Utara-Tengah (UNSULUTTENG) Manado di Gorontalo berdasarkan surat keputusan pejabat Rektor UNSULUTTENG Nomor 1313/II/E/63 tanggal 22 Juni 1963, Cabang FKIP UNSULUTTENG di Gorontalo.

Kemudian pada 1964 berubah menjadi Cabang FKIP IKIP Yogyakarta Cabang Manado dan pada tahun 1965 bergabung dengan IKIP Manado Cabang Gorontalo.

Lembaga ini juga pernah menjadi salah satu Fakultas dari Universitas Sam Ratulangi Manado dengan nama Fakultas Keguruan dan Ilmu Pendidikan (FKIP) Unsrat Manado di Gorontalo.

Barulah pada 1993 lembaga ini berdiri sendiri dengan nama Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) Gorontalo.

Kemudian pada 2001, status lembaga ini ditingkatkan menjadi IKIP Negeri Gorontalo dengan 5 Fakultas dan 25 Program Studi. (1)

Perubahan IKIP Negeri Gorontalo menjadi Universitas Negeri Gorontalo ditetapkan dengan surat Keputusan Presiden RI nomor 54 tahun 2004 tanggal 23 Juni 2004.

Hari lahir UNG ditetapkan sama dengan lahirnya cabang FKIP UNSULUTTENG di Gorontalo yaitu, tanggal 1 September 1963 sebagaimana dinyatakan dalam surat keputusan menteri PTIP nomor 67 tahun 1963 tanggal 11 Juli 1963.