• Metode Iterasi Titik tetap

Metode Iterasi Titik tetap kadang-kadang dinamakan metode iterasi sederhana atau metode langsung atau metode substitusi beruntun. Kesederhanaan metode ini karena pembentukan prosedur iterasinya yang mudah dibentuk, yaitu kita ubah persamaan f (x) = 0 menjadi bentuk x = g(x), kemudian dibentuk menjadi prosedur iterasi,Metode iterasi titik tetap termasuk metode terbuka. Artinya dalam menghampiri akar, metode ini tidak memerlukan selang tertutup seperti metode bagi dua dan metode posisi palsu. Kita dapat mentransformasikan fungsi f(x) = 0 dalam bentuk x = g(x). Prosedur iterasi yang berpadanan adalah x_n+1 = g(x_n) dengan fungsi g seperti yang diperoleh dalam bentuk x = g(x). Suatu selesaian dalam bentuk tersebut disebut suatu titik tetap dari g. Untuk suatu persamaan f(x) = 0 yang diberikan mungkin berpadanan dengan beberapa persamaan x = g(x) akan tetapi bisa menghasilkan kekonvergenan barisan x₀, x₁, x₂, x₃, … yang mungkin berbeda, tergantung dari pemilihan x₀.Berikut ini langkah penyelesaian Iterasi Titik Tetap:

1.Susunlah persamaan f (x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi: 

x_n+1 = g(x_n)

2.Tentukan nilai awal x0.

3.Lakukan iterasi dengan menghitung nilai

   x₁ = g(x₀), x₂ = g(x₁), x₃ = g(x₂)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

 f (k) = 0 ; k = g(k)

4.Cek konvergensi terhadap XTOL (jika ada).

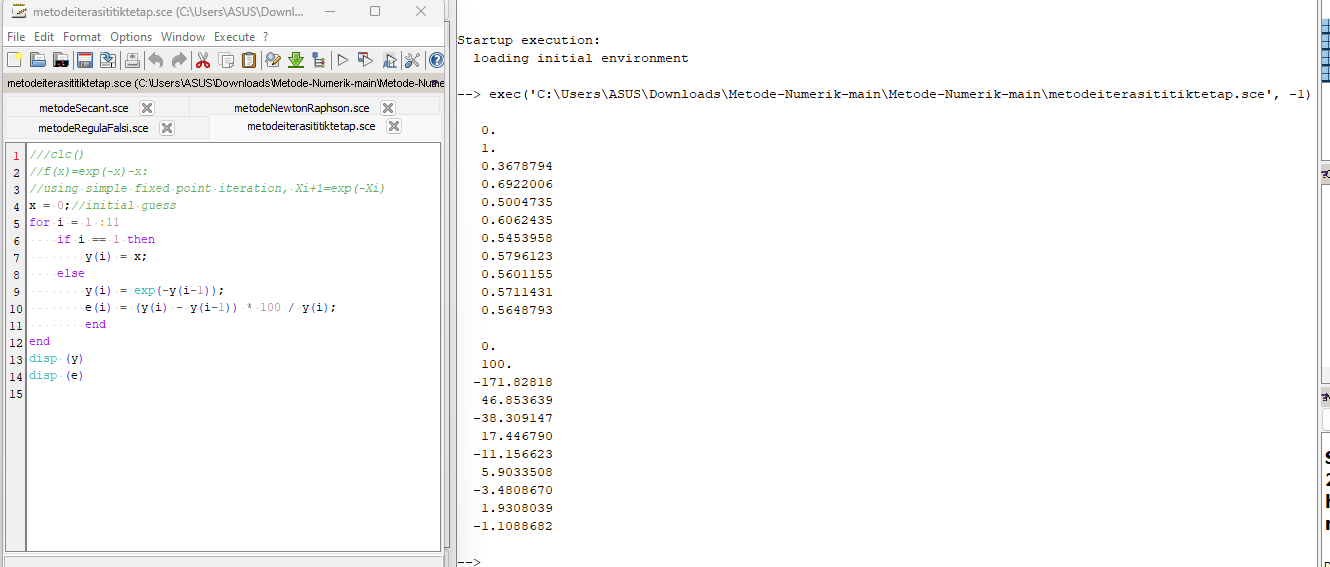
Berikut ini adalah contoh program Scilab untuk mencari akar persamaan f(x)=exp(-x)-x menggunakan metode iterasi titik tetap sederhana sampai iterasi 10 dan x₀ = 0:

• Metode Regulasi Falsi

Metode regula falsi atau metode posisi palsu merupakan salah satu solusi pencarian akar dalam penyelesaian persamaan-persamaan non linier melaui proses iterasi (pengulangan). Persamaan non linier ini biasanya berupa persamaan polynomial tingkat tinggi, eksponensial, logaritmik, dan kombinasi dari persamaan-persamaan tersebut. Seperti metode biseksi, Metode regula falsi juga termasuk dalam metode tertutup. Pada umumnya pencarian akar dengan metode biseksi selalu dapat menemukan akar, namun kecepatan untuk mencapai akar hampiran sangat lambat, oleh karena itu untuk mempercepat pencarian akar tersebut dibutuhkan metode lain yaitu metode regula falsi. kehadiran metode regula falsi adalah sebagai modifikasi dari metode biseksi, yang kinerjanya lebih cepat dalam mencapai akar hampiran.Berikut ini langkah penyelesaian metode Regulasi Falsi:

1. Tentukan nilai awal a dan b

2. Cek konvergensi a dan b

3. Lakukan iterasi

4. Hitung nilai c diantara a dan b, dimana :

c = a .f ( b ) - b . f ( a ) / f ( b ) - f ( a )    

5. Cek Konvergensi nilai c   

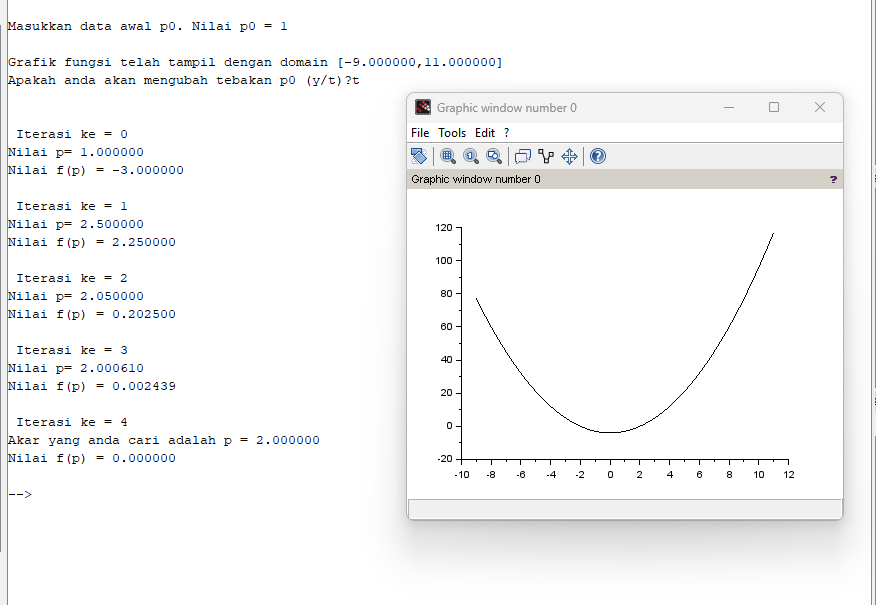
 Berikut ini adalah contoh program Scilab untuk mencari akar persamaan f(x)=x^2-4=(x-2)(x+2) menggunakan metode iterasi titik tetap epsilon = 0,00001 dan x₀ = 1:

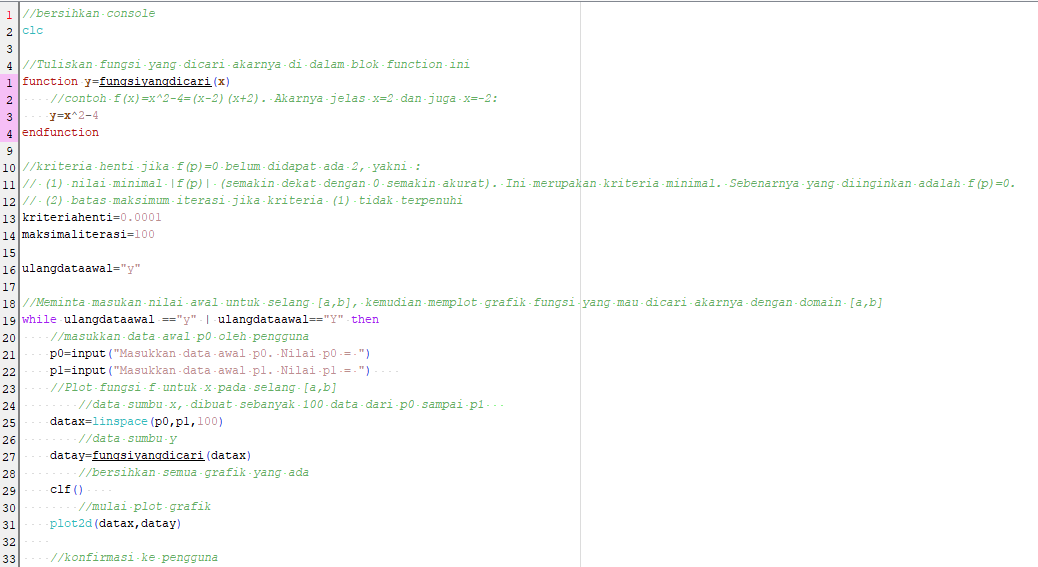
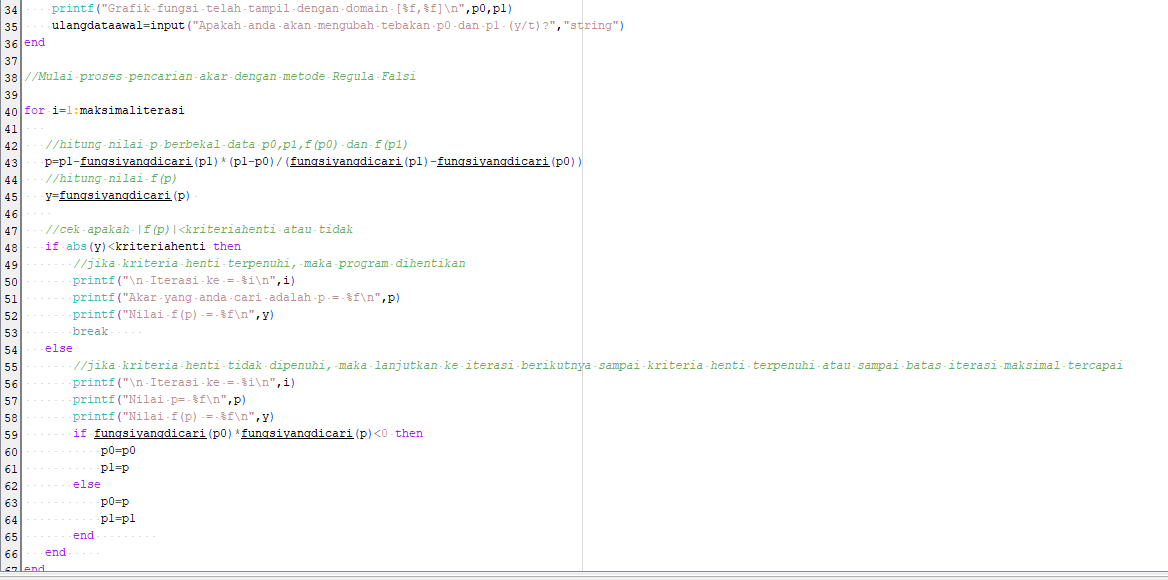
Hasil dan Grafik Hasil

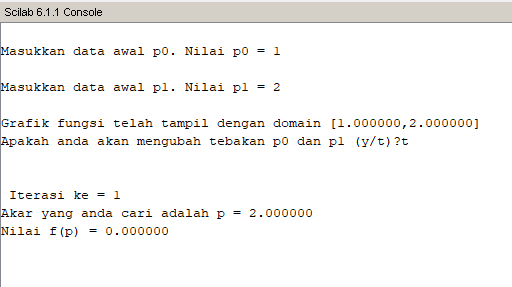
• Metode Secant

Metode Secant merupakan modifikasi metode Newton-Raphson. Pada metode Newton-Raphson, pada setiap proses iterasinya memerlukan perhitungan nilai dua buah fungsi, yakni f(x_n) dan f’(x_n). Apabila kedua fungsi tersebut tidak rumit, metode tersebut mungkin sangat baik mengingat kekonvergenannya. Akan tetapi, tidak semua fungsi dapat diturunkan dengan mudah, terutama fungsi-fungsi yang rumit.Sedangkan metode Secant hanya memerlukan satu fungsi saja yaitu f(x_n), yang jika pemrogramannya dilakukan dengan benar, maka nilainya dapat diperoleh dari iterasi sebelumnya f(x_n-1). Sehingga metode Secant akan memerlukan waktu yang lebih sedikit untuk tiap iterasinya dari pada metode Newton.Berikut langkah penyelesaian metode Secant:

1.Tentukan nilai awal x₀ dan x₁

2. Hitung f(x₀) dan f(x₁)

3. Lakukan iterasi 

4. Hitung nilai taksiran akar selanjutnya

 

 

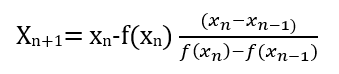
5. Cek konvergensi terhadap XTOL (Jika ada)

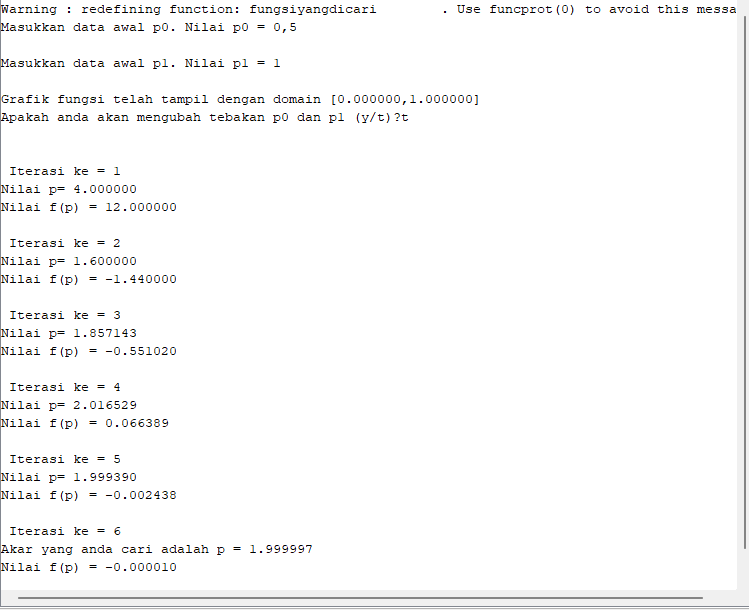
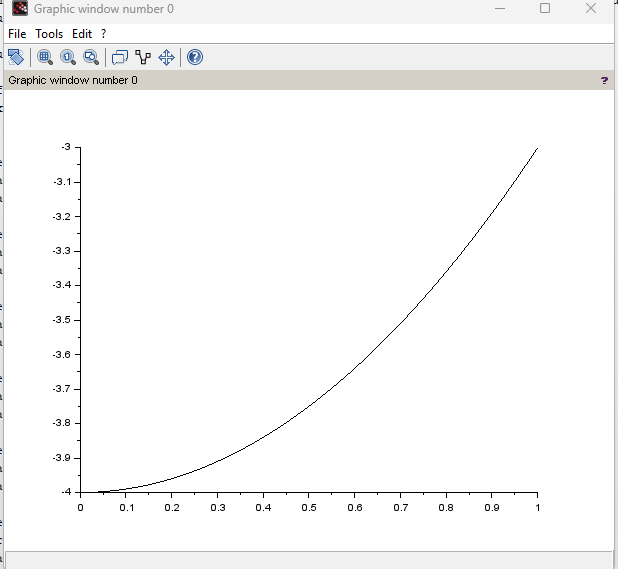
Berikut ini adalah contoh program Scilab untuk mencari akar persamaan f(x)=x^2-4=(x-2)(x+2) menggunakan metode iterasi titik tetap epsilon = 0,00001 dan x₀ = 0,5:

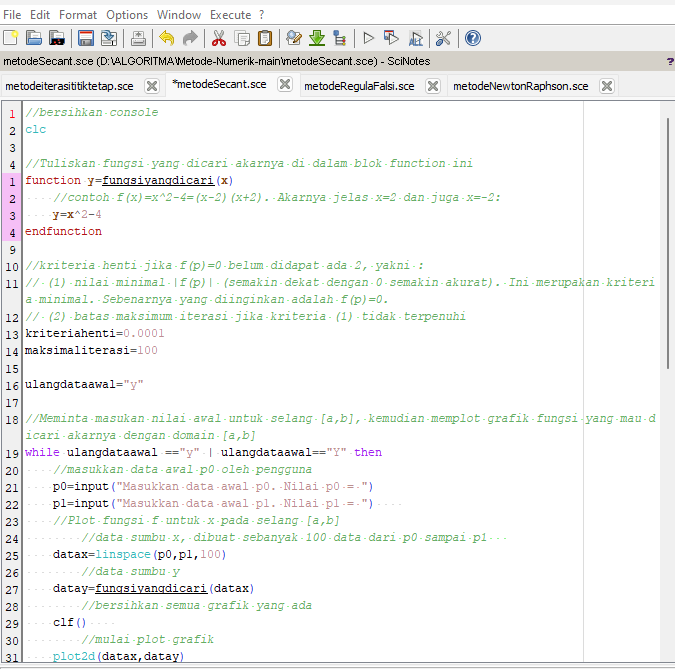
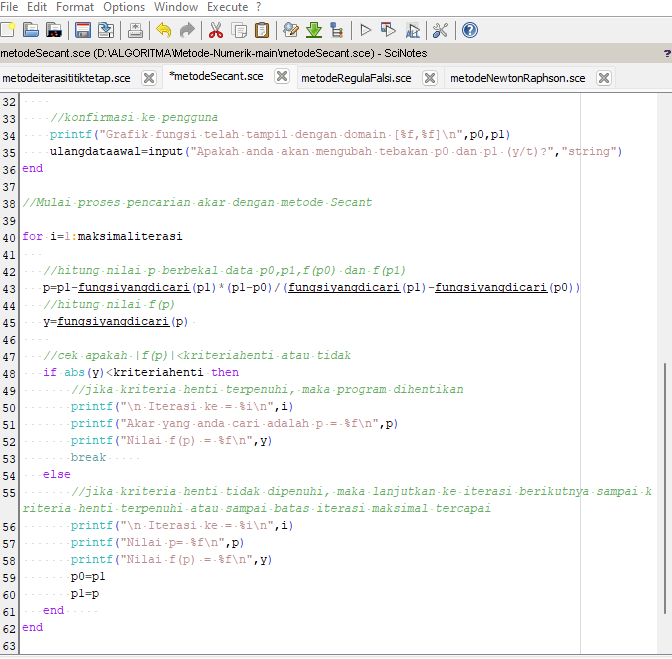
Hasil dan grafik hasil

• Metode Newton-Rapshon

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.Berikut langkah penyelesaian metode Newton-Rapshon:

1. Tentukan nilai awal x₀

2. Hitung f (x₀) kemudian cek konvergensi f (x₀)

3. Tentukan fungsi f'(x₀),kemudian hitung f'(x₀)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

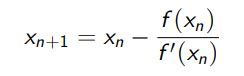
6. Cek konvergensi terhadapa XTOL (Jika ada)

Berikut ini adalah contoh program Scilab untuk mencari akar persamaan f(x)=x^2-4=(x-2)(x+2) menggunakan metode iterasi titik tetap epsilon = 0,00001 dan x₀ = 1:

 

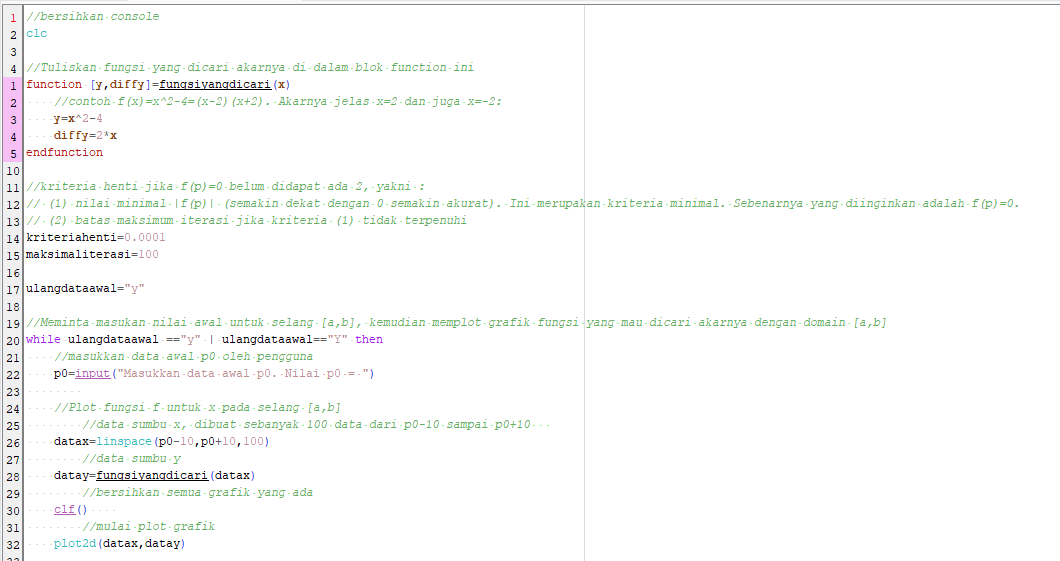
Hasil dan Grafik Hasil