Penyelesaian Persamaan NonLinier dapat dilakukan dalam 2 cara, yaitu :• Metode Tertutup– Mencari akar pada range [a,b] tertentu– Dalam range[a,b] dipastikan terdapat satu akar– Hasil selalu konvergen maka disebut juga metode konvergen

• Metode Terbuka– Diperlukan tebakan awal– xn dipakai untuk menghitung xn+1– Hasil dapat konvergen atau divergen

1. Metode Regulasi Falsi

metode pencarian akar persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dua titik batas range. Dua titik a dan b pada fungsi f(x) digunakan untuk mengestimasi posisi c dari akar interpolasi linier. Metode ini juga dikenal dengan metode False Position.

Langkah-langkah Metode Regulasi Falsi :

1. Tentukan nilai awal a dan b

2. Cek konvergensi nilai f(a) dan f(b)

• Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnya
• Jika tanda f(a) = tanda f(b), pilih nilai awal yang baru

3. Lakukan iterasi

4. Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))

5. Cek konvergensi nilai c

• Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| 
• Jika nilai Cn dan Cn-1 konstan
• Jika nilai f(Cn) = 0

6. Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c akan menggantikan a
• Jika tanda f(c) = tanda f(b) maka c akan menggantikan b

Perhitungan menggunakan aplikasi Scilab :

Berikut syntax untuk metode regulasi falsi:

 

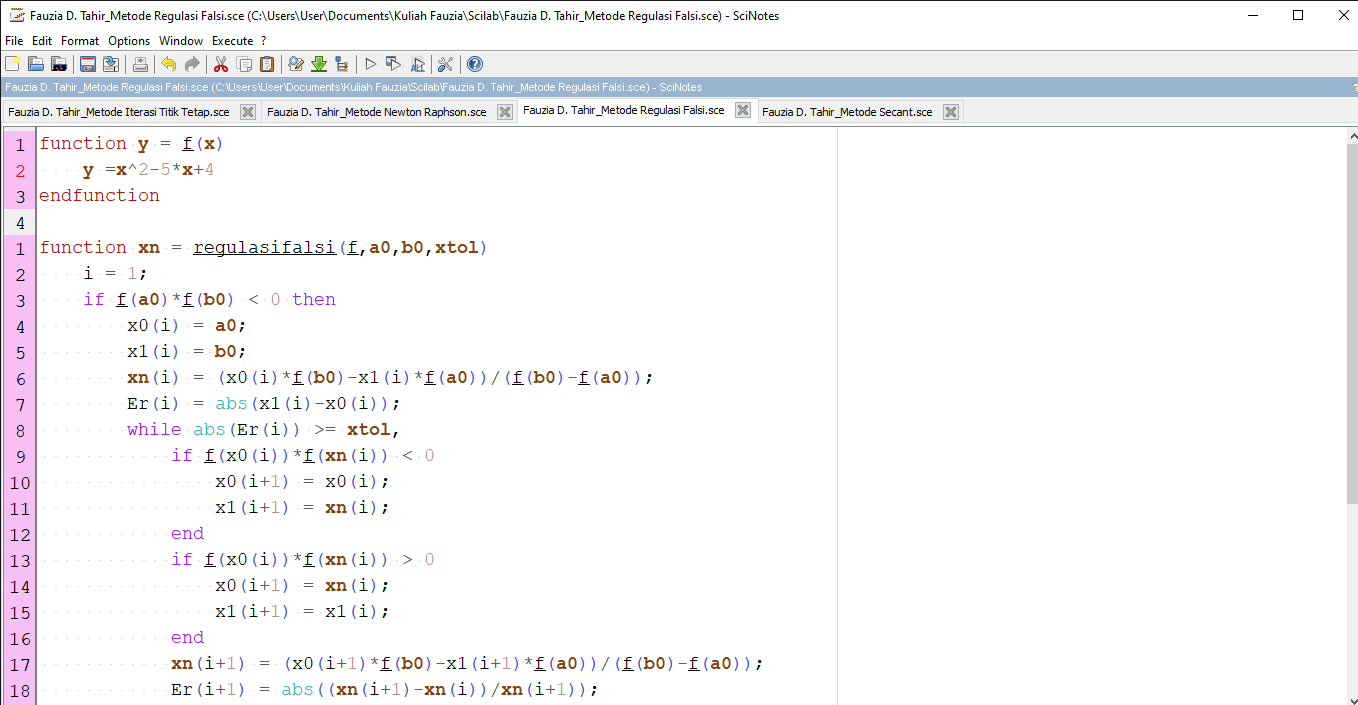
Diperoleh hasil :

 

 

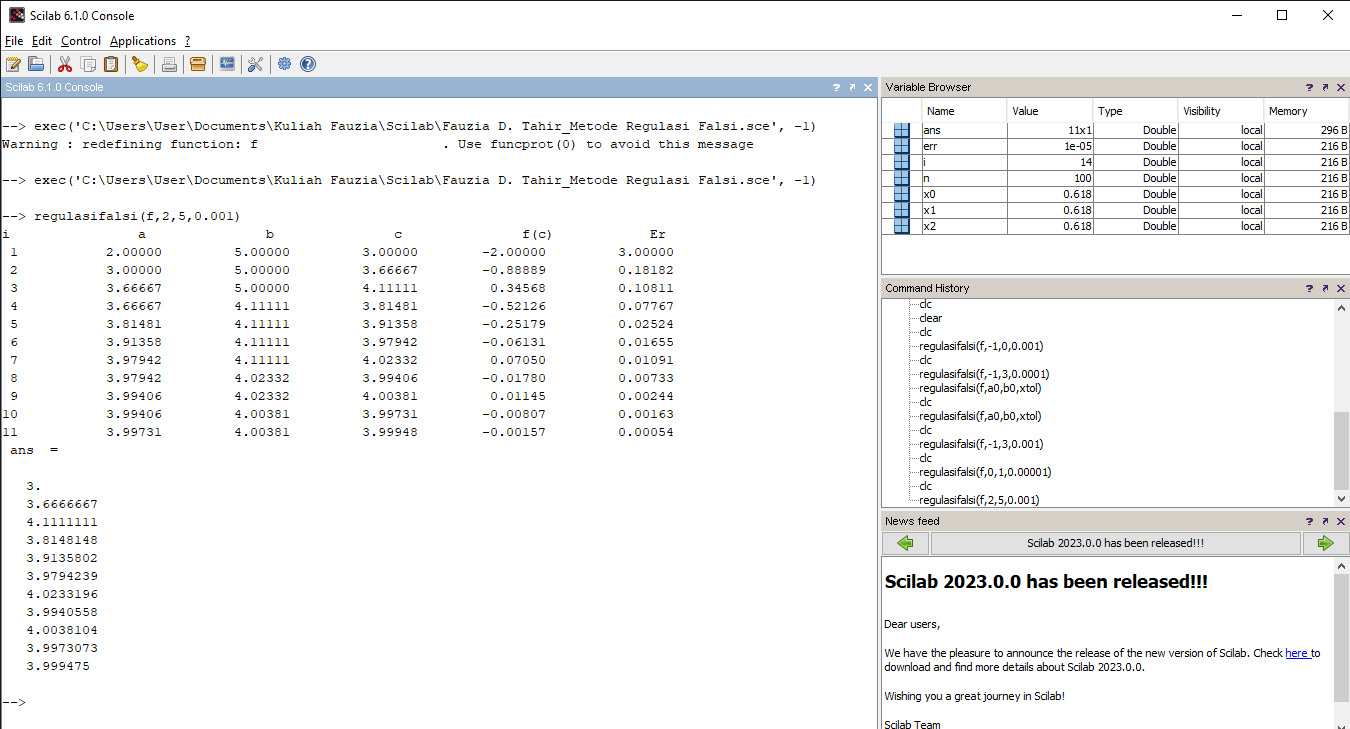
2. Metode Iterasi Titik Tetap

Metode iterasi sederhana adalah metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh : x = g(x).

• g(x) inilah yang menjadi dasar iterasi pada metode iterasi titik tetap ini

Langkah-langkah Metode Iterasi Titik Tetap:

1. Susunlah persamaan f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:                             

                                                                    xn+1 = g(xn)

2. Tentukan nilai awal x0.

3. Lakukan iterasi dengan menghitung nilai x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

                                                        f (k) = 0 ; k = g(k)

4. Cek konvergensi terhadap XTOL (jika ada).

 

Perhitungan menggunakan aplikasi Scilab :

 

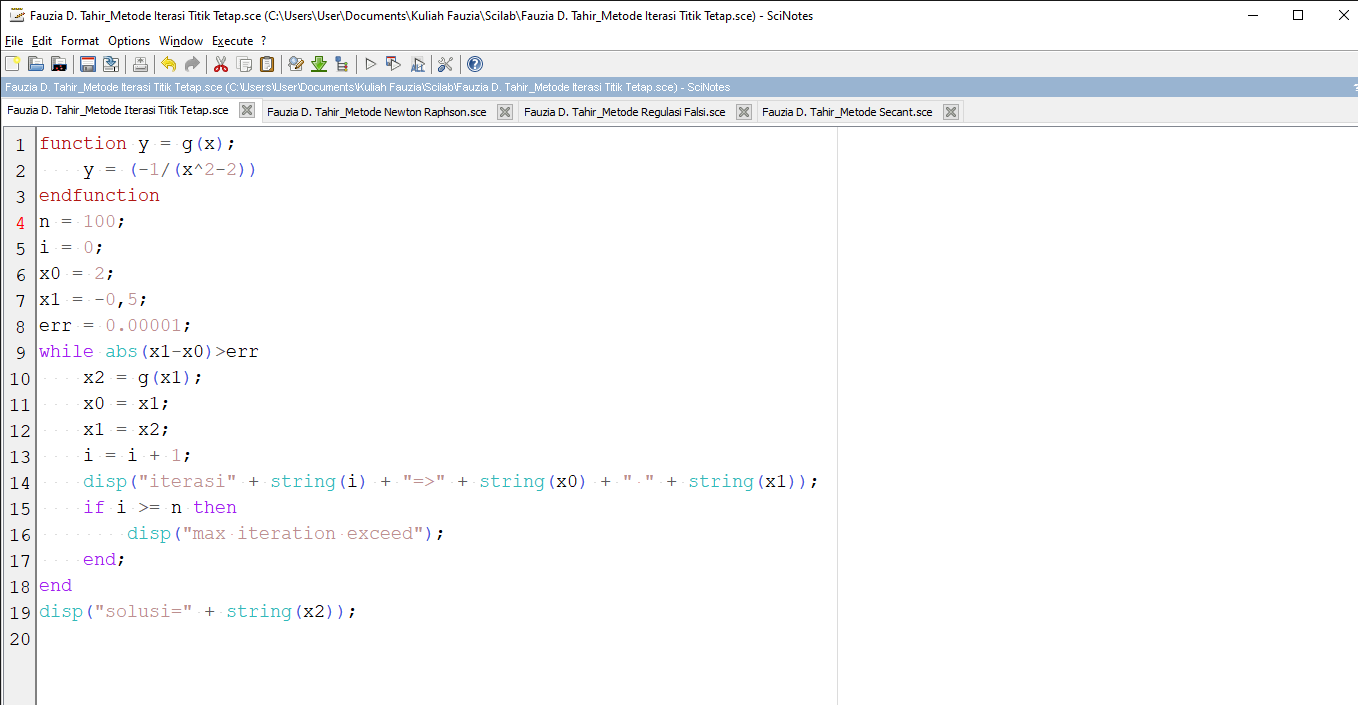
Diperoleh Hasil : 

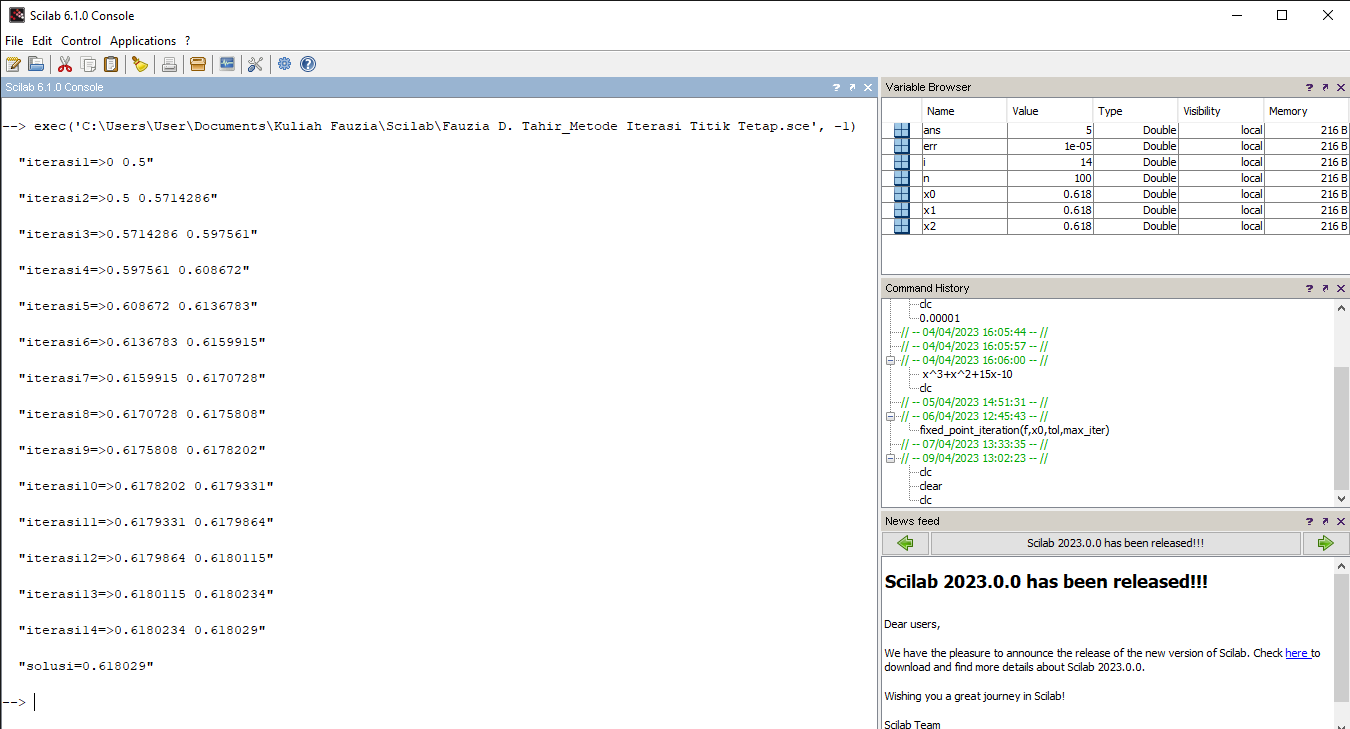
3. Metode Newton-Raphson

Langkah-langkah Metode Newton-Raphson:

1. Tentukan nilai awal x0

2. Hitung f(x0) kemudian cek konvergensi f(x0)

3. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

 Sintax pada Scilab :

 

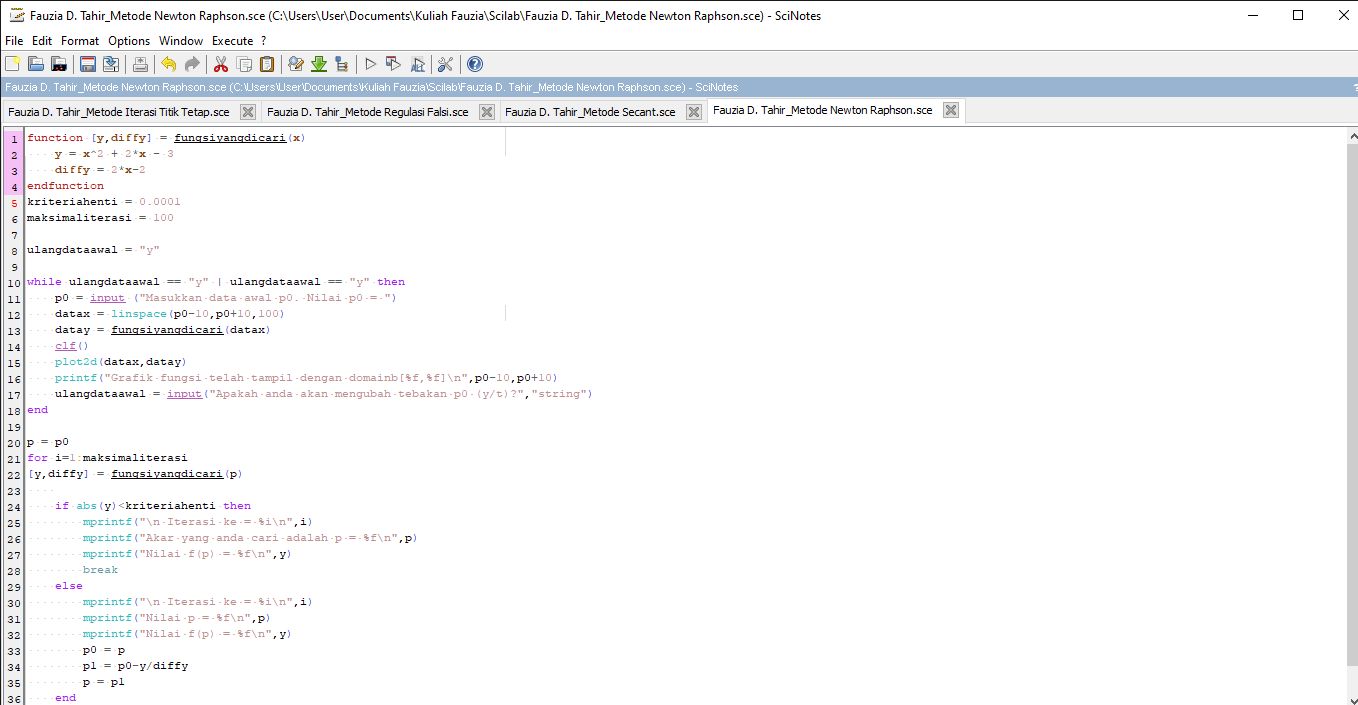
Hasilnya adalah :

 

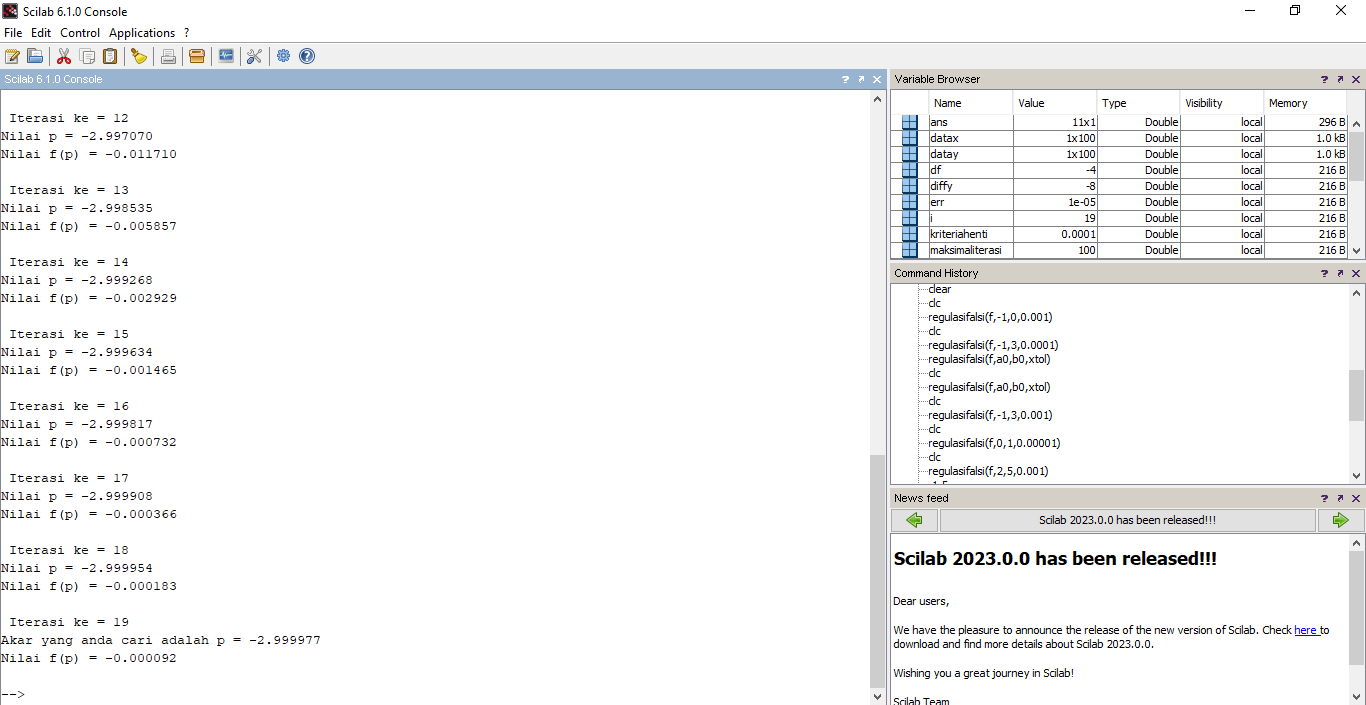
4. Metode Secant

Metode Newton Raphson memerlukan perhitungan turunan fungsi f’(x).• Tidak semua fungsi mudah dicari turunannya terutama fungsi yang bentuknya rumit.• Turunan fungsi dapat dihilangkan dengan cara menggantinya dengan bentuk lain yang ekivalen• Modifikasi metode Newton Raphson dinamakan metode Secant.

Sintax Metode Secant pada Scilab:

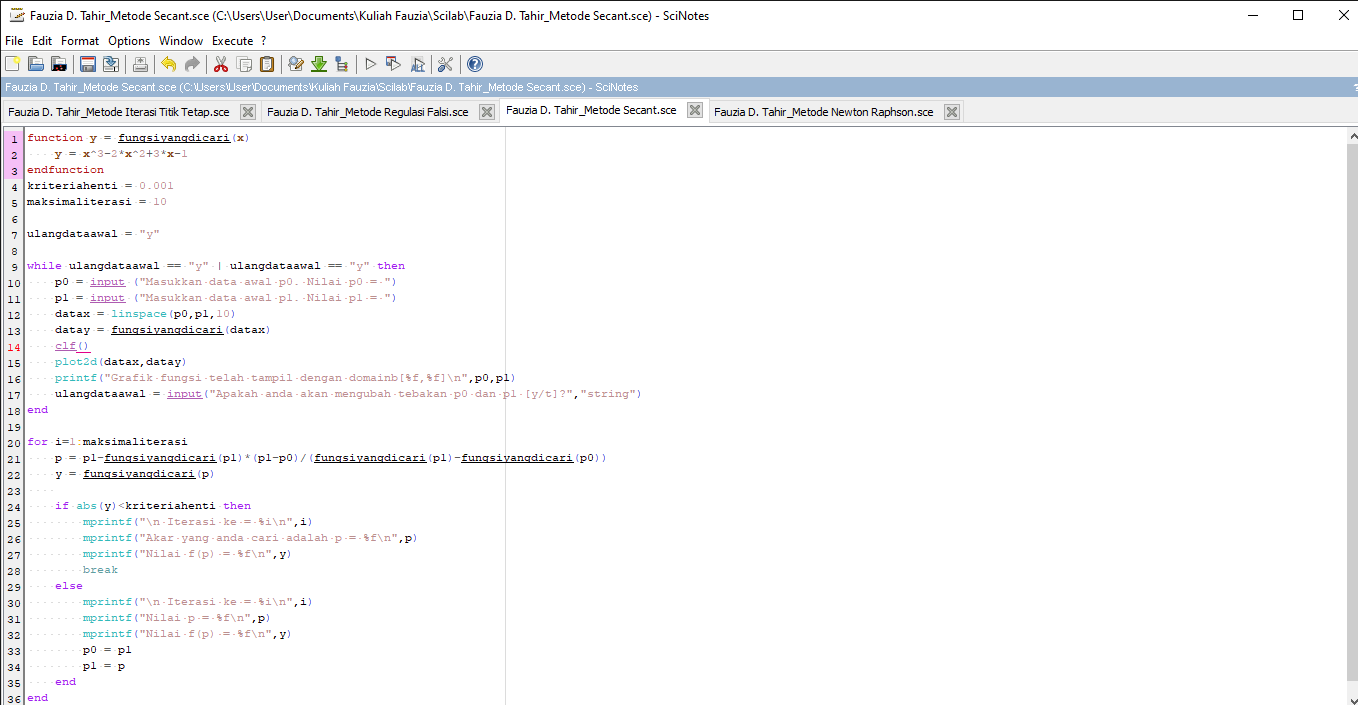
Hasil : 

 

 

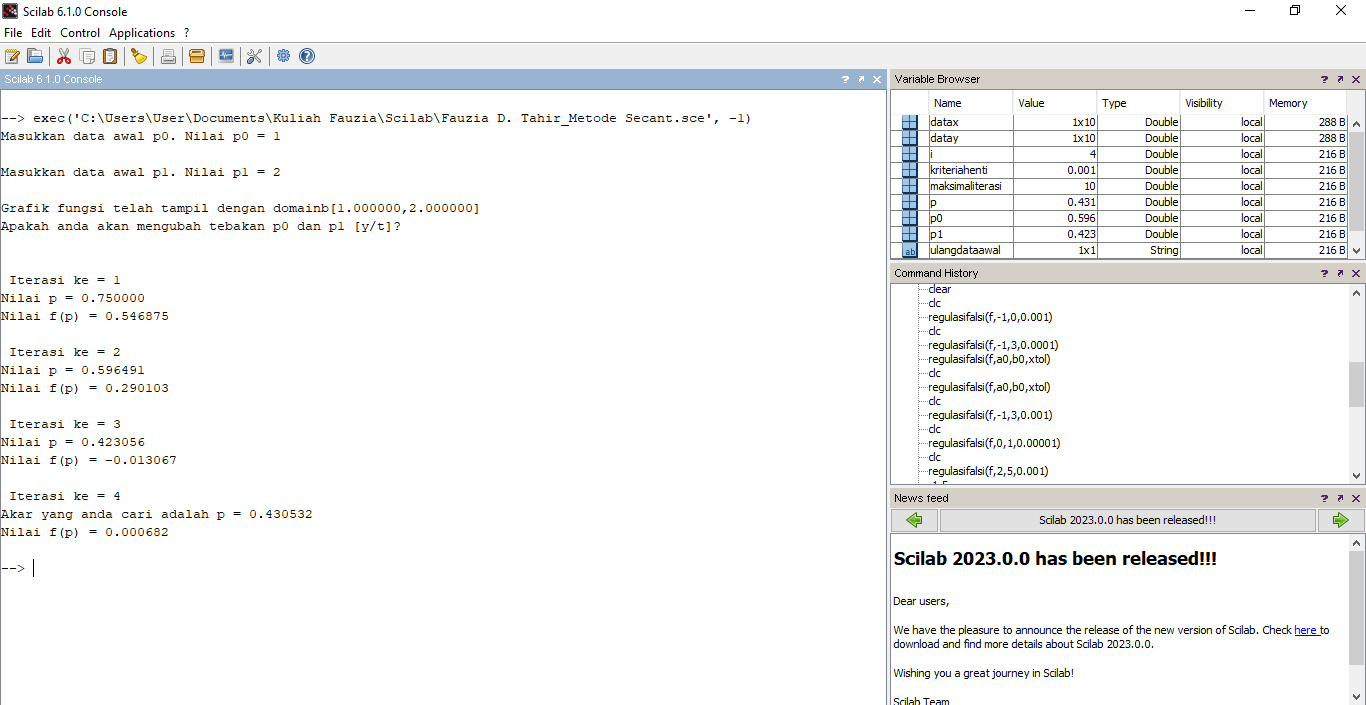
Demikian uraian penjelasan mengenai pencarian akar persamaan takl inear  pada aplikasi scilab dalam  beberapa metode tertutup dan terbuka. Lebih dan kurangnya saya mohon maaf.

Semoga bermanfaat:)