Dalam Blog ini kita akan membahas terkait penggunakan metode regulasi falsi, metode iterasi titik tetap, metode newton rapshon dan metode secant dengan menggunakan scilab programming dalam hal kita akan membahas tekait pembuatan syntax untuk mencari pemecahan solusi dengan cara numerik.

Masalah pencarian akar persamaan nonlinier, menemukan akar persamaan nonlinier secara analitik sulit dilakukan, kecuali dalam kasus yang lebih sederhana. Oleh karena itu, diperlukan pendekatan numerik untuk menyelesaikan masalah yang tidak dapat diselesaikan secara analitik. Oleh karena itu, diperlukan metode numerik untuk menyelesaikan permasalahan dalam ilmu pengetahuan dan teknologi.

Pada metode numerik proses pencarian akar dapat dilakukan dengan dua cara yaitu metode tertutup dan metode terbuka. Metode tertutup disebut juga dengan metode root fixing karena proses pencarian akar dilakukan pada interval tertutup [a,b]. Metode tertutup terdiri dari:

• metode bisection
• metode regulasi falsi
• Metode Iterasi Titik Tetap

sedangkan metode tertutup terdiri dari :

• metode newton-rapshon
• metode secant

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dari dua titik batas range. Sebenarnya metode ini hampir sama dengan Metode Biseksi, tapi titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi.

Langkah-langkah Metode Regulasi Falsi :

1. Tentukan nilai awal a dan b
2. Cek konvergensi nilai f(a) dan f(b) Jika tanda f(a) tidak sama dengan tanda f(b), nilai dapat digunakan untuk iterasi selanjutnyaJika tanda f(a) = tanda f(b), pilih nilai awal yang baru
3. Lakukan iterasi
4. Hitung nilai c diantara a dan b, dimana c = (a.f(b)-b.f(a))/(f(b)-f(a))
5. Cek konvergensi nilai c

Jika terdapat XTOL, bandingkan XTOL dengan Erc = |Cn-Cn-1| / |Cn| Jika nilai Cn dan Cn-1 konstanJika nilai f(Cn) = 06. Jika belum konvergen juga, tentukan nilai awal baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c akan menggantikan aJika tanda f(c) = tanda f(b) maka c akan menggantikan b
• Perhitungan menggunakan aplikasi Scilab.

Selanjutnya kita akan membahas penggunaan metode regulasi falsi dalam hal ini kita menggambil contoh masalah persamaan polinom dengan menggunkan pemecahan masalah numerik :

y = x^3 + 5*x^2 + 8*x - 26

Berikut syntax scilab untuk metode Regulasi Falsi :

 

 

 

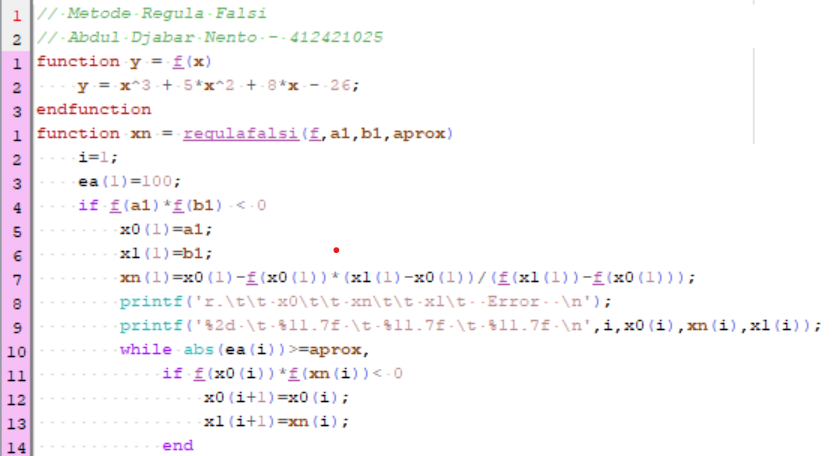
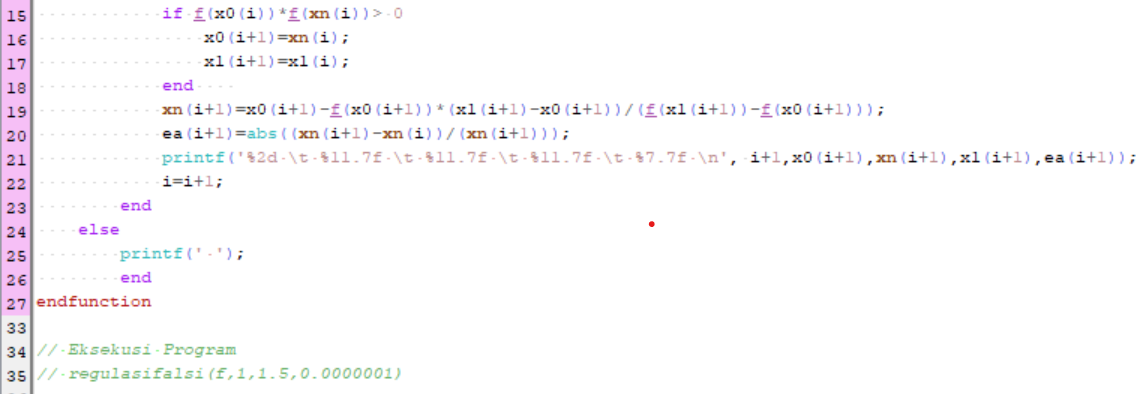
2. Metode Iterasi titik tetap

Metode Iterasi Titik tetap kadang-kadang dinamakan metode iterasi sederhana atau metode langsung atau metode substitusi beruntun. Kesederhanaan metode ini karena pembentukan prosedur iterasinya yang mudah dibentuk, yaitu kita ubah persamaan f (x) = 0 menjadi bentuk x = g(x), kemudian dibentuk menjadi prosedur iterasi

Metode iterasi titik tetap termasuk metode terbuka. Artinya dalam menghampiri akar, metode ini tidak memerlukan selang tertutup seperti metode bagi dua dan metode posisi palsu. Kita dapat mentransformasikan fungsi f(x) = 0 dalam bentuk x = g(x). Prosedur iterasi yang berpadanan adalah xn+1 = g(xn) dengan fungsi g seperti yang diperoleh dalam bentuk x = g(x). Suatu selesaian dalam bentuk tersebut disebut suatu titik tetap dari g. Untuk suatu persamaan f(x) = 0 yang diberikan mungkin berpadanan dengan beberapa persamaan x = g(x) akan tetapi bisa menghasilkan kekonvergenan barisan x0, x1, x2, x3, … yang mungkin berbeda, tergantung dari pemilihan x0.

Langkah-langkah Metode Iterasi Titik Tetap:

1. Susunlah persamaan  f(x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi:                             

                                                                    xn+1 = g(xn)

2. Tentukan nilai awal x0.

3. Lakukan iterasi dengan menghitung nilai

x1 = g(x0), x2 = g(x1), x3 = g(x2)... yang mudah-mudahan konvergen ke akar sejati k, sehingga:

f (k) = 0 ; k = g(k)

4. Cek konvergensi terhadap XTOL (jika ada)

Berikut syntax scilab untuk metode Iterasi Titik Tetap :

 

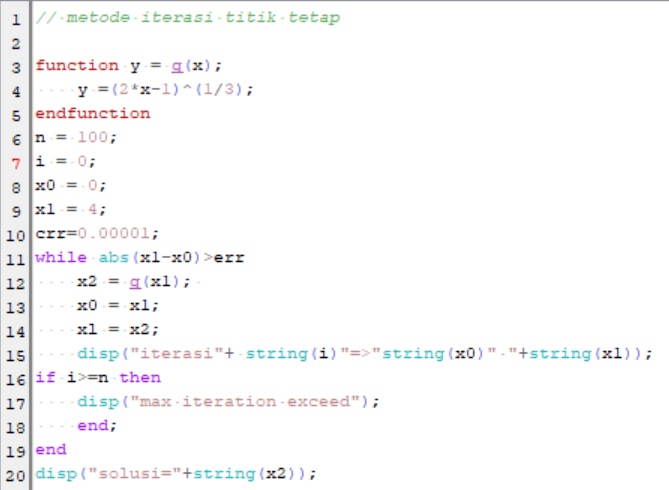
3. Metode Newton-Rhapson

Dalam analisis numerik, metode Newton (juga dikenal sebagai metode Newton-Raphson), yang mendapat nama dari Isaac Newton dan Joseph Raphson, merupakan metode yang paling dikenal untuk mencari hampiran terhadap akar fungsi riil.

Metode Newton sering konvergen dengan cepat, terutama bila iterasi dimulai “cukup dekat” dengan akar yang diinginkan. Namun bila iterasi dimulai jauh dari akar yang dicari, metode ini dapat meleset tanpa peringatan. Implementasi metode ini biasanya mendeteksi dan mengatasi kegagalan konvergensi.Diketahui fungsi ƒ(x) dan turunannya ƒ ‘(x), kita memulai dengan tebakan pertama, x 0.

Langkah-langkah Metode Newton-Raphson:

1. Tentukan nilai awal x0

2. Hitung f(x0) kemudian cek konvergensi f(x0)

3. Tentukan fungsi f'(x0), kemudian hitung f'(x0)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

                 xn+1 = xn - (f(xn)/f'(xn))

6. Cek konvergensi terhadapa XTOL (Jika ada)

Berikut Syntax Dengan Menggunakan Scylab :

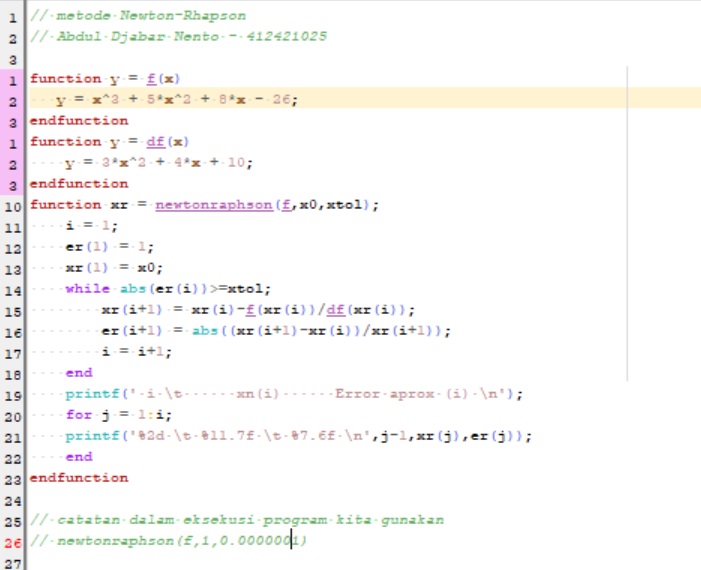
4. Metode Secant

Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.ujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f‘ (x).Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.

Algoritma Metode Secant

1. Definisikan fungsi F(x)
2. Definisikan torelansi error (e) dan iterasi maksimum (n)
3. Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.
4. Hitung F(x0) dan F(x1) sebagai y0 dan y1
5. Untuk iterasi I = 1 s/d n atau |F(xn)| Xn+1 = Xn – Yn (Xn – Xn-1 / Yn – Yn-1)

Berikut adalah Syuntax dari Metode Secant:

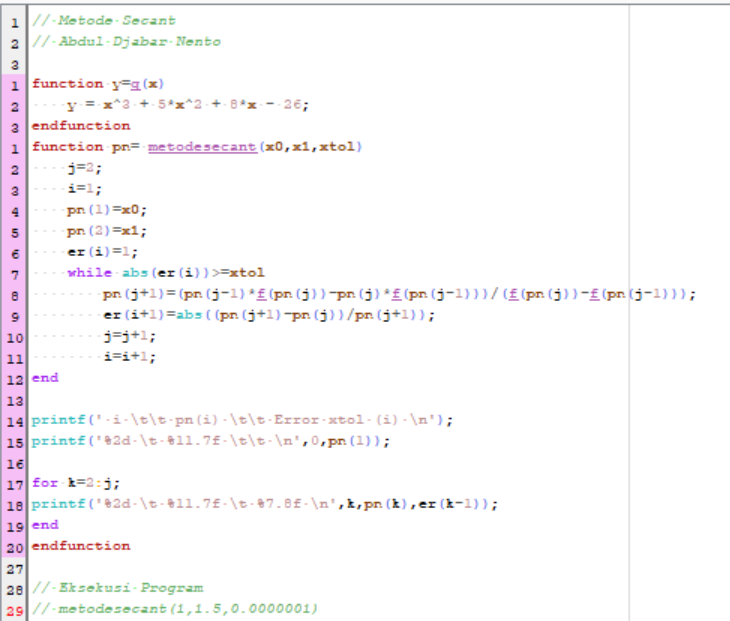
Demikian uraian penjelasan langkah-langkah beserta syntax dari masing-masing metode pada aplikasi scilab dalam pencarian akar persamaan tak linear. Lebih dan kurangnya saya mohon maaf.

Semoga bermanfaat:)