Dalam blog kali ini kita akan mengerjakan soal-soal 5.9 Latihan Mandiri 

1. Pada soal pertama kita di minta untuk membuat program penjumlahan (bagian A) dan pengurangan (bagian B) matriks tanpa memanfaatkan fungsi yang terdapat di library (tanpa Numpy) dan dengan penggalan algoritma yang merupakan sebuah pseudocode (yaitu instruksi yang mirip dengan bahasa pemrograman tetapi bukan merupakan sintaks yang langsung bisa dijalankan di Python atau bahasa pemrograman lainnya. Pseudocode bertujuan untuk memberikan gambaran logika dan struktur dasar dari algoritma tanpa harus mematuhi aturan sintaksis spesifik. Sehingga kita akan membuat program dengan menerjemahkan penggalan algoritmanya kedalam bahasa pemograman Pyhton).

Baik mari kita masuk pada langkah-langkah pembuatannya

• Inisialisasi Matriks A dan B Sesuai Ukuran yang Diperlukan

 

Pada bagian ini, kita memulai dengan meminta pengguna memasukkan jumlah baris (m) dan kolom (n) yang diinginkan untuk matriks A dan B. Hasilnya disimpan dalam variabel m dan n, yang nanti digunakan untuk membuat matriks dan mengontrol jumlah elemen yang harus dimasukkan.

 

• Membuat Matriks A dengan Memasukkan Input 

 

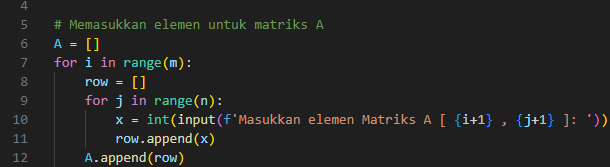
Di sini, kita membuat matriks A dengan cara sebagai berikut:

• A = []: Inisialisasi matriks A sebagai list kosong.
• for i in range(m): Loop ini berjalan sebanyak m kali untuk mengisi setiap baris matriks.
• row = []: Membuat list row kosong untuk menyimpan elemen-elemen satu baris.
• for j in range(n): Loop ini berjalan sebanyak n kali untuk mengisi kolom pada setiap baris.
• x = int(input(...)): Meminta pengguna memasukkan elemen tertentu pada posisi [i+1, j+1] dan mengonversinya ke integer.
• row.append(x): Menambahkan elemen ke dalam row.
• A.append(row): Setelah satu baris penuh, row ditambahkan ke dalam matriks A sebagai satu baris.

 

• Menampilkan Matriks A yang Telah Diisi

 

Pada bagian ini, kita menampilkan matriks A yang telah diisi dengan elemen-elemen matriks. Dengan for row in A, setiap baris dari A dicetak dalam format yang rapi menggunakan print.

 

•  Membuat Matriks B dengan Input Pengguna (Sama dengan Langkah pada Matriks A)

 

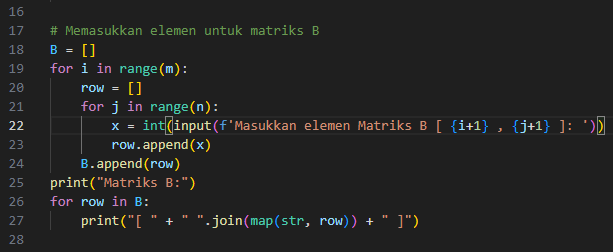
Langkah ini hampir identik dengan blok untuk matriks A, hanya saja perbedaan terdapat pada input yang meminta elemen matriks B. Proses dan cara penyimpanan elemennya sama.

 

 

(Masuk Pada Bagian A)

•  Inisialisasi Matriks Hasil Penjumlahan atau Matriks C dengan Nol

 

Di sini, kita menyiapkan matriks C dengan ukuran m×n yang terisi nol di setiap elemennya. Matriks C ini akan digunakan untuk menyimpan hasil penjumlahan A+B.

 

• Menjumlahkan Elemen Matriks A dan B ke dalam Matriks C

 

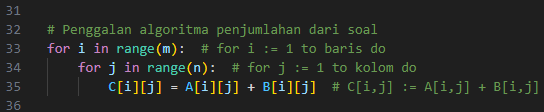
Blok ini melakukan operasi penjumlahan untuk setiap elemen dari matriks A dan B:

• for i in range(m) dan for j in range(n): Dua loop untuk mengakses setiap elemen matriks berdasarkan posisi [i, j].
• C[i][j] = A[i][j] + B[i][j]: Menambahkan elemen pada posisi [i, j] di A dan B, lalu hasilnya disimpan di matriks C.

 

• Menampilkan Hasil Penjumlahan Matriks A + B

 

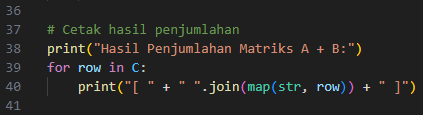
Pada bagian ini, kita menampilkan hasil penjumlahan matriks C dalam format matriks agar mudah dilihat oleh pengguna.

 

 

(Masuk pada bagian B)

• Inisialisasi Matriks Hasil Pengurangan D dengan Nol

 

Blok ini melakukan operasi pengurangan setiap elemen pada matriks A dengan elemen pada matriks B dan menyimpannya dalam matriks D.

 

• Mengurangkan Elemen Matriks A dan B ke dalam Matriks D

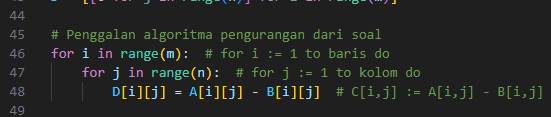
Blok ini melakukan operasi pengurangan setiap elemen pada matriks A dengan elemen pada matriks B dan menyimpannya dalam matriks D

 

• Menampilkan Hasil Pengurangan Matriks A - B

 

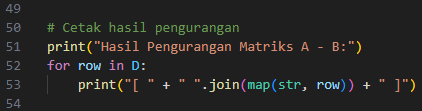
Terakhir, kita menampilkan hasil dari pengurangan matriks D dengan format rapi agar mudah dibaca oleh pengguna.

 

2. Sekarang kita lanjut pada soal Kedua, hampir sama seperti pada soal pertama yang membuat program penjumlahan dan pengurangan matriks, pada soal kedua kita diminta untuk membuat program yang dapat mengalikan matriks.

Mari kita lihat langkah-langkah pembuatannya.

• Input Ukuran Matriks A

 

Bagian ini meminta pengguna memasukkan ukuran matriks A berupa jumlah baris m_A dan jumlah kolom n_A.

 

• Inisialisasi Matriks A

 

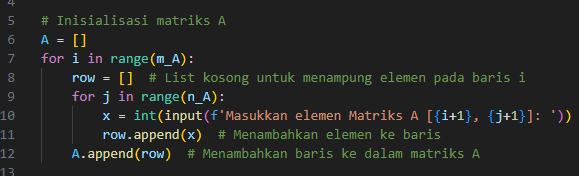
Di sini, matriks A diisi berdasarkan masukan pengguna:

• A = []: Membuat list kosong A yang akan menyimpan setiap baris matriks.
• Loop pertama (for i in range(m_A)) mengatur jumlah baris pada A.
• Di dalam loop, row = [] membuat list kosong row untuk menampung elemen-elemen pada satu baris.
• Loop kedua (for j in range(n_A)) mengisi row dengan elemen yang diinput pengguna satu per satu.
• A.append(row): Setelah satu baris selesai, row ditambahkan ke dalam A.

 

• Cetak Matriks A

 

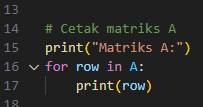
Bagian ini menampilkan matriks A dalam format yang mudah dibaca. Setiap baris matriks ditampilkan satu per satu.

 

• Input Ukuran Matriks B

 

Karena jumlah kolom pada A harus sama dengan jumlah baris pada B agar perkalian matriks bisa dilakukan, variabel n_B (jumlah baris pada B) disamakan dengan n_A. Pengguna hanya perlu memasukkan jumlah kolom untuk matriks B, yaitu p_B.

 

• Inisialisasi Matriks B

 

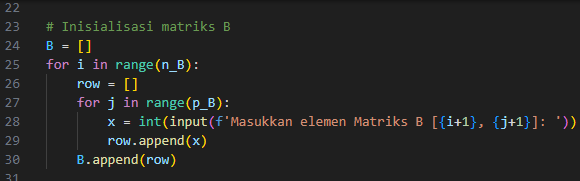
Proses inisialisasi matriks BBB mirip dengan inisialisasi matriks A, hanya saja ukuran baris matriks B sesuai n_B dan kolom sesuai p_B. Elemen-elemen B dimasukkan sesuai posisi [i+1, j+1].

 

• Cetak Matriks B

 

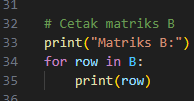
Bagian ini menampilkan matriks B setelah diisi elemen-elemen dari pengguna.

 

• Inisialisasi Matriks Hasil C dengan Nol

 

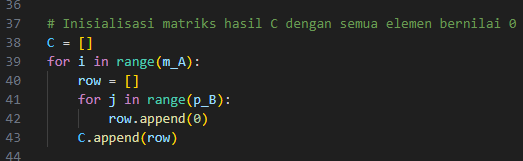
Matriks C diinisialisasi dengan ukuran mA X  pB dan diisi dengan nilai nol sebagai tempat menyimpan hasil perkalian A X B.

 

• Algoritma Perkalian Matriks

 

Di sini, algoritma untuk perkalian matriks dilakukan:

• for i in range(m_A): Mengakses setiap baris pada A.
• for j in range(p_B): Mengakses setiap kolom pada B.
• C[i][j] = 0: Inisialisasi elemen C[i][j] dengan nol sebelum pengisian.
• for k in range(n_A): Untuk melakukan perkalian elemen yang bersesuaian antara baris A dan kolom B.
• C[i][j] += A[i][k] * B[k][j]: Menambahkan hasil perkalian elemen A[i][k] dan B[k][j] ke posisi C[i][j].

 

• Cetak Hasil Perkalian Matriks A * B

 

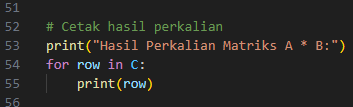
Terakhir, hasil perkalian matriks C ditampilkan dengan format yang rapi untuk memudahkan pengguna melihat hasil dari operasi A X B.

 

 Baik itu dia penjelasan mengenai jawaban terhadap soal-soal pada 5.9 Latihan Mandiri

python