Metode Numerik adalah teknik-teknik yang digunakan untuk dapat memformulasikan masalah matematis supaya dapat dipecahkan dengan operasi perhitungan. Metode Numerik tersebut penting disebabkan karna mengajarkan untuk dapat memecahkan suatu kasus dengan memakai berbagai cara serta permodelan.Metode numerik juga merupakan suatu sarana yang efisien untuk mempelajari penggunaan komputer dan aplikasi lainnya.Metode numerik mampu menyelesaikan suatu sistim persamaan yang besar, persamaan yang tidak linier dan persamaan yang kompleks yang tidak mungkin diselesaikan secara analitis. 

Penyelesaian numerik dilakukan dengan iterasi, sehingga setiap hasil yang didapat selalu lebih teliti dibandingkan iterasi sebelumnya. Ada beberapa metode yang digunakan untuk menghitung akar-akar persamaan yaitu:

1. Metode Bisection
2. Metode Regula Falsi 
3. Metode Newton-Raphson
4. Metode Secant
5. Metode Iterasi Titik Tetap

Dalam kesempatan kali ini saya akan menunjukan perhitungan beberapa metode menggunaan aplikasi scilab.

1. Metode Regulasi Falsi

Metode Regula Falsi adalah salah satu metode numerik yang digunakan untuk mencari akar dari suatu persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dari dua titik batas range. Sebenarnya metode ini hampir sama dengan Metode Biseksi, tapi titik pendekatan yang digunakan pada metode ini berbeda dengan Metode Biseksi.

Langkah-langkah Metode Regulasi Falsi :

1. Tentukan nilai awal interval [a, b].
2. Cek konvergensi nilai f(a) dan f(b).
3. Lakukan iterasi dan tentukan nilai c (hitung akar)
4. Cek konvergensi nilai c, jika nilai f(c) = 0 dan nilai cn+1 dan cn konstan, maka proses iterasi dihentikan.
5. Jika belum konvergen, tentukan nilai interval baru dengan cara:

• Jika tanda f(c) = tanda f(a) maka c = a  
• Jika tanda f(c) = tanda f(b) maka c = b

Perhitungan menggunakan aplikasi Scilab :

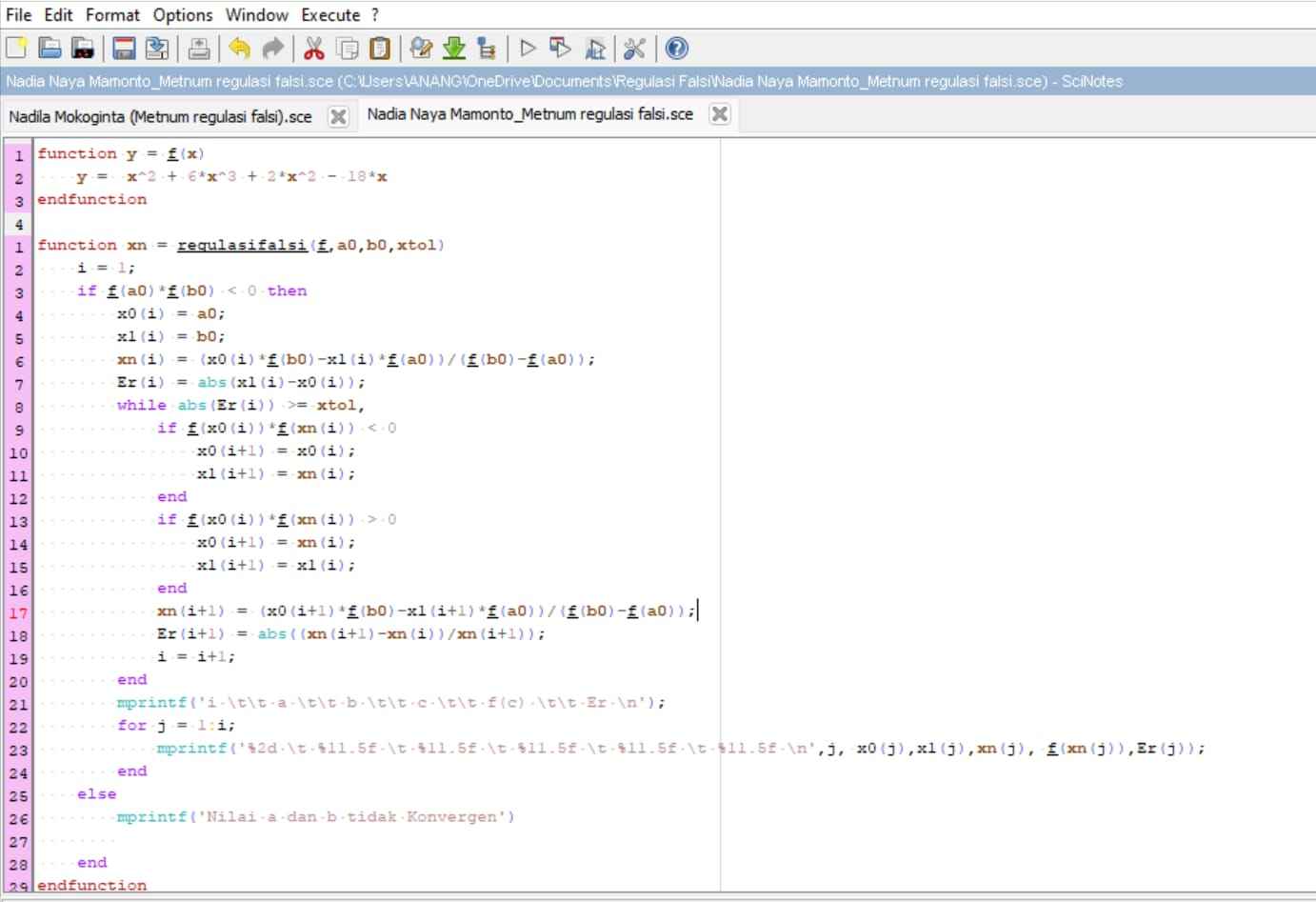
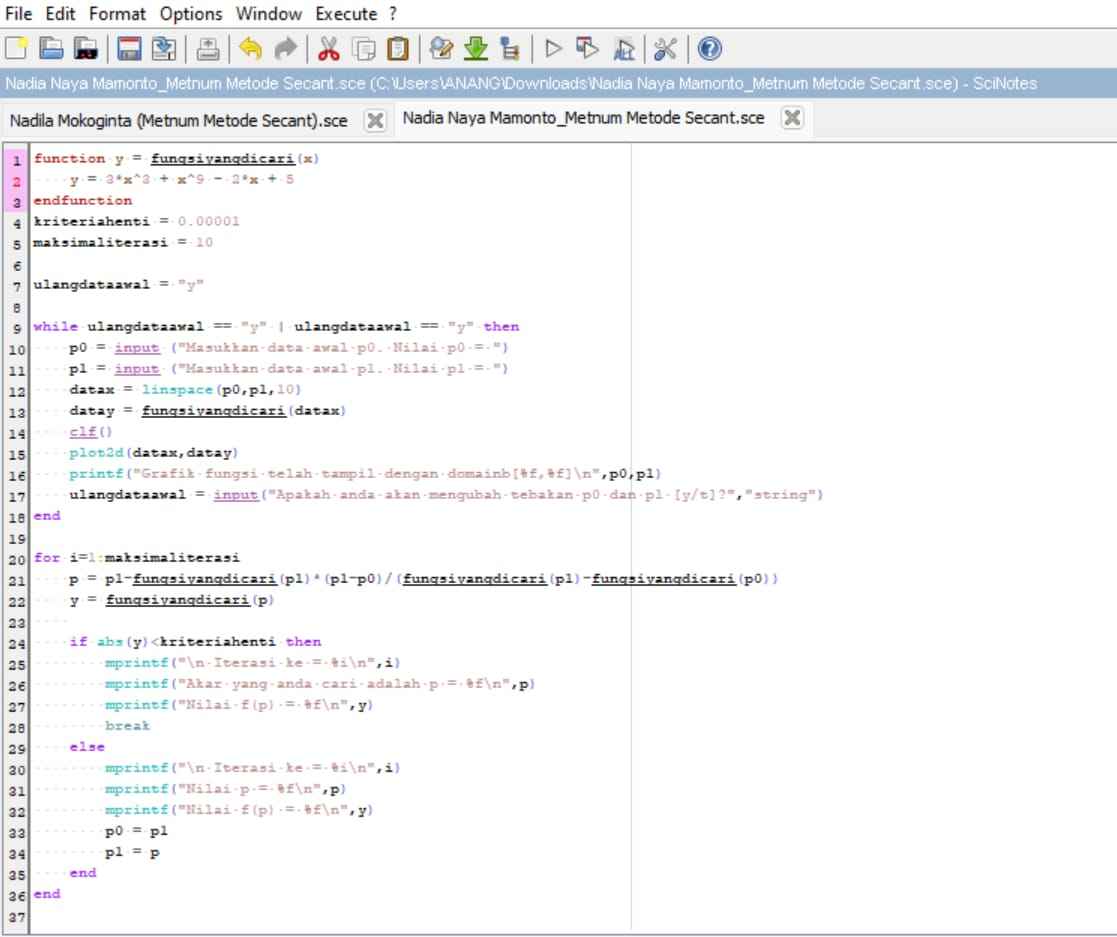
2. Metode Secant

Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f'(x). Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.

Langkah-langkah Metode Secant: 

1. Tentukan x0, x1, toleransi, dan jumlah iterasi maksimum.
2. Hitung Xbaru = X1 - f(x1)( x1- x0)/f(x1) – f(x0).
3. Jika nilai mutlak (xbaru - x1) < toleransi, diperoleh tulisan xbaru sebagai hasil perhitungan.
4. Jika tidak, lanjutkan ke langkah berikutnya.
5. Jika jumlah iterasi > iterasi maksimum, akhiri program.
6. x = xbaru, dan kembali ke langkah (2).

Perhitungan menggunakan aplikasi Scilab :

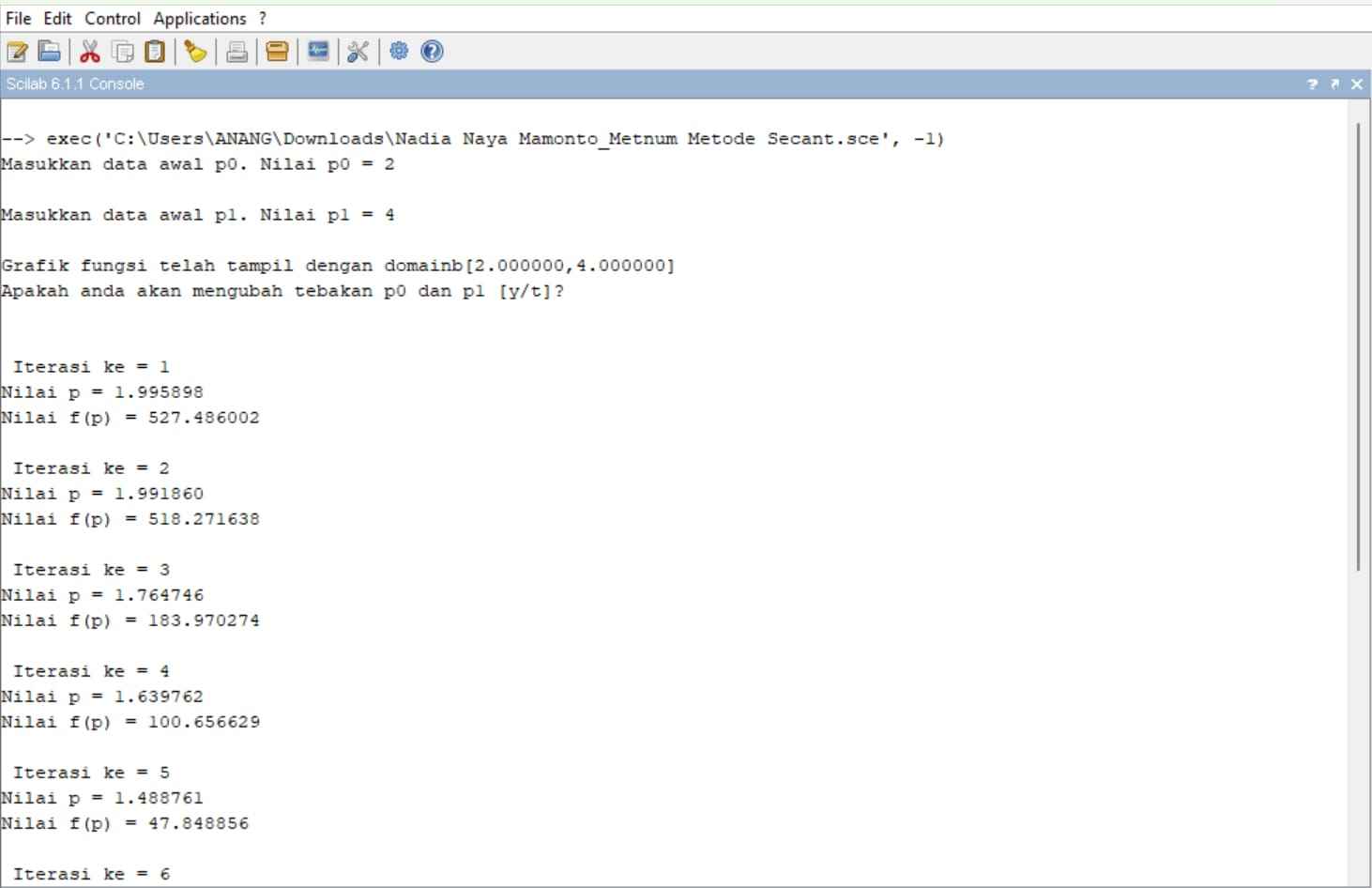
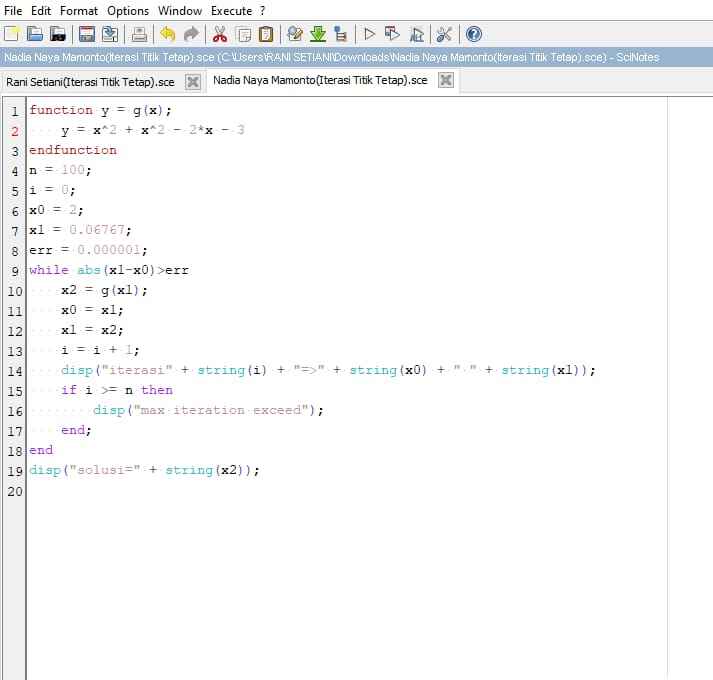
3. Metode Iterasi Titip Tetap

Metode iterasi titik tetap merupakan metode penyelesaian persamaan non-linier dengan cara menyelesaikan setiap variabel xx yang ada dalam suatu persamaan dengan sebagian yang lain sehingga diperoleh x=g(x)x=g(x) untuk masing-masing variabel xx. Sebagai contoh, untuk menyelesaikan persamaan x+ex=0x+ex=0, maka persamaan tersebut perlu diubah menjadi x=exx=ex atau g(x)=exg(x)=ex.

Langkah-langkah Metode Iterasi Titik Tetap :

1. Ubah persamaan f(x) = 0 menjadi bentuk x = g(x)
2. Bentuk menjadi prosedur iterasi xn+1 = g(xn)
3. Tentukan sebuah nilai tawal x0
4. Hitung nilai x1,x2,x3,..., yang konvergen ke suatu titik s.

Perhitungan menggunakan aplikasi Scilab :

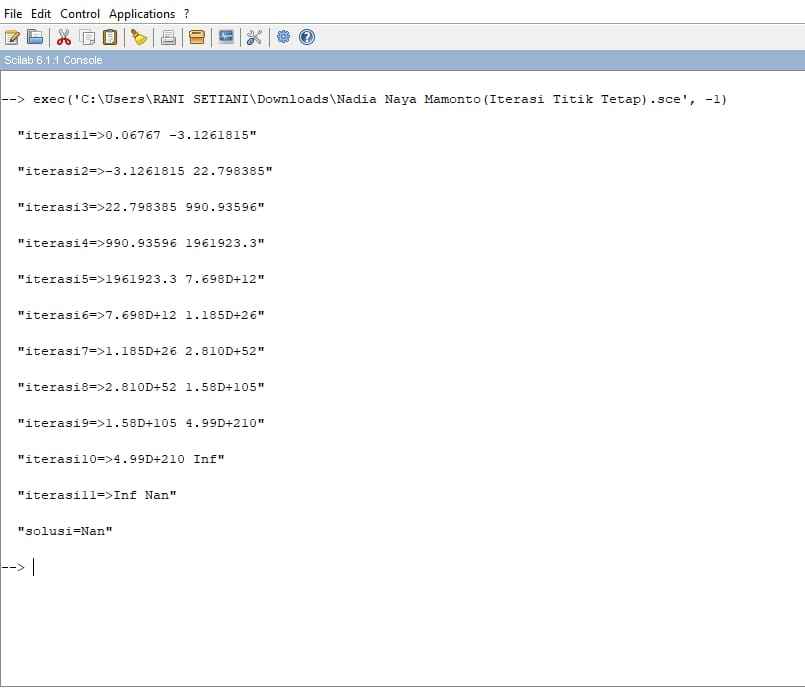
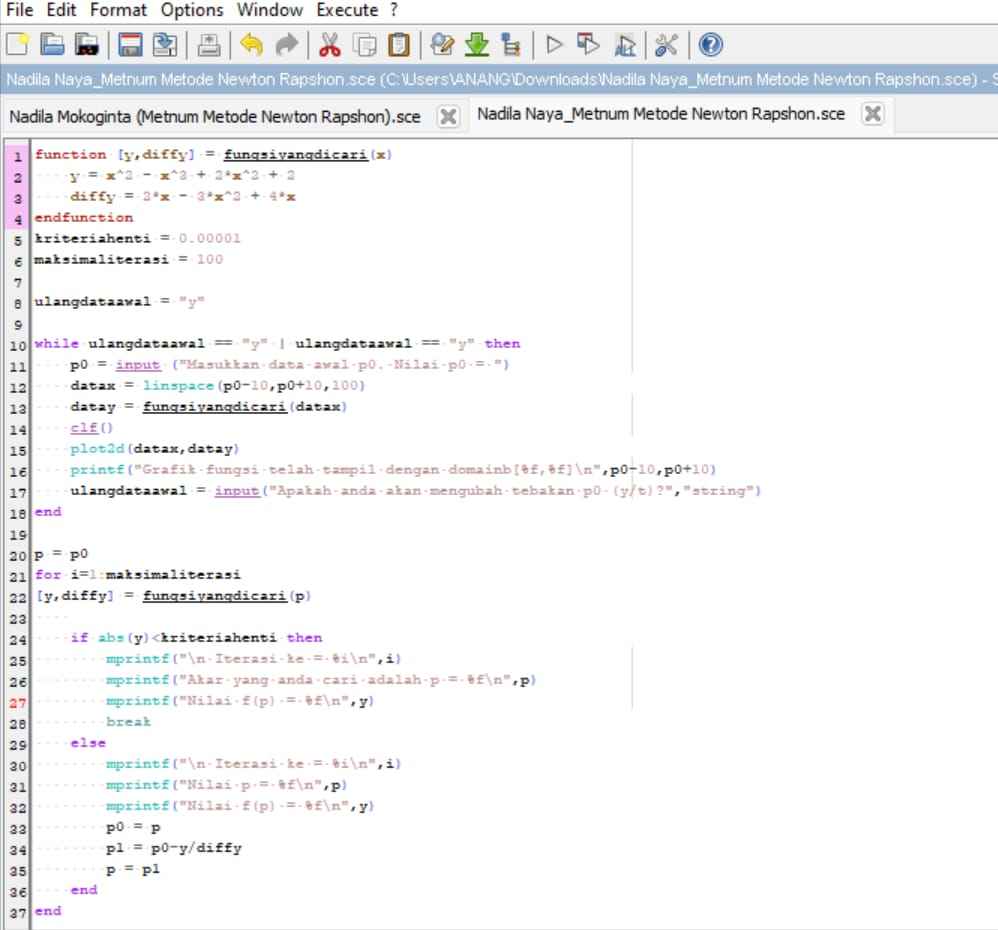
4. Metode Newton-Raphson

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

1. Langkah-langkah Metode Newton-Raphson:
2. Tentukan titik awal x0
3. Hitung f(x0) dan f'(x0)
4. Hitung xn = x0 - f(x0)/f'(x0) ; f'(x0) 0,n = 1,2,3,…
5. Iterasi lebih besar atau sama dengan iterasi maksimum tulis xhampiran = xn, jika tidak lanjut ke langkah selanjutnya.
6. Ganti nilai x0 = xn dan kembali ke langkah 4.

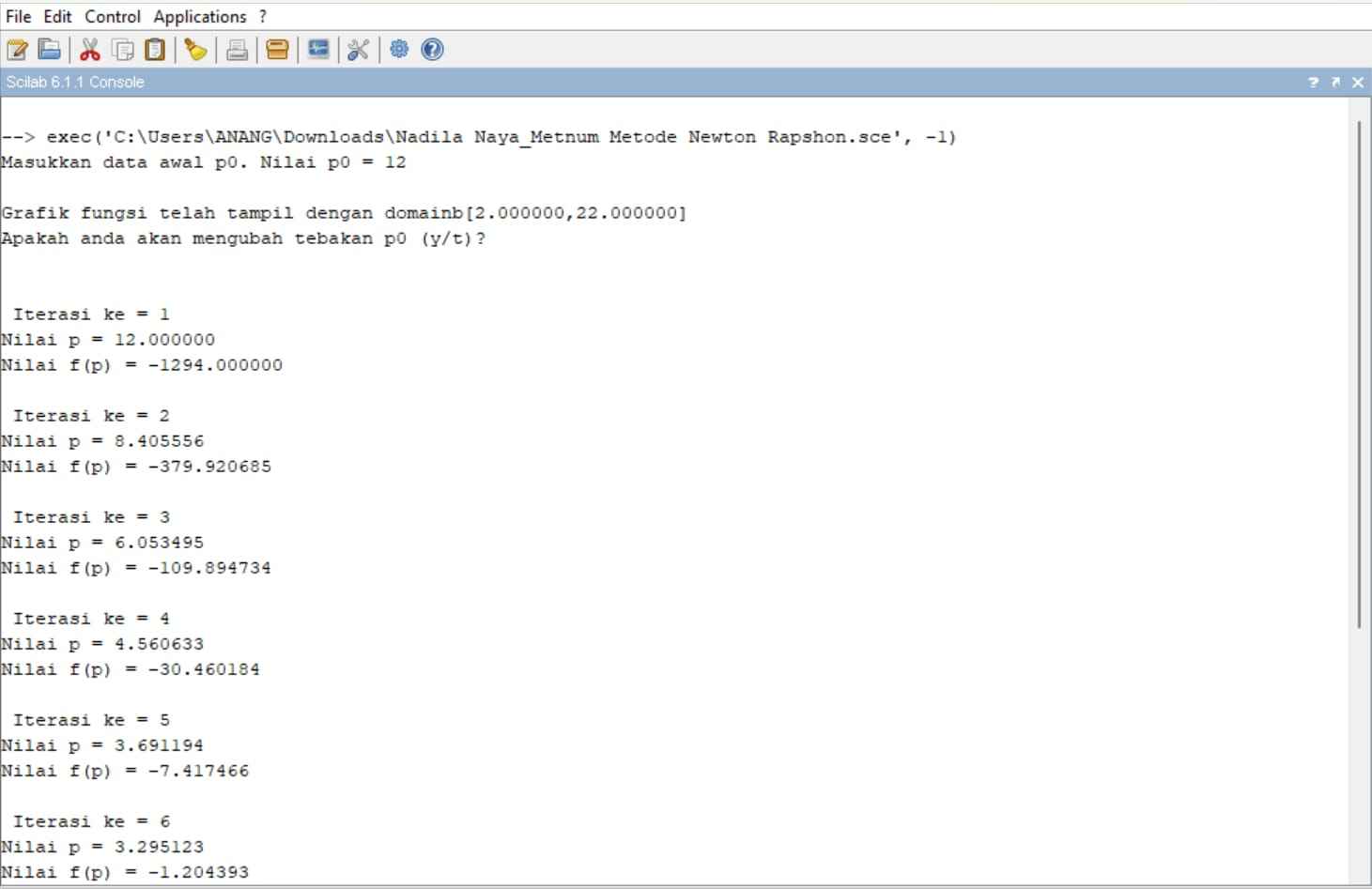
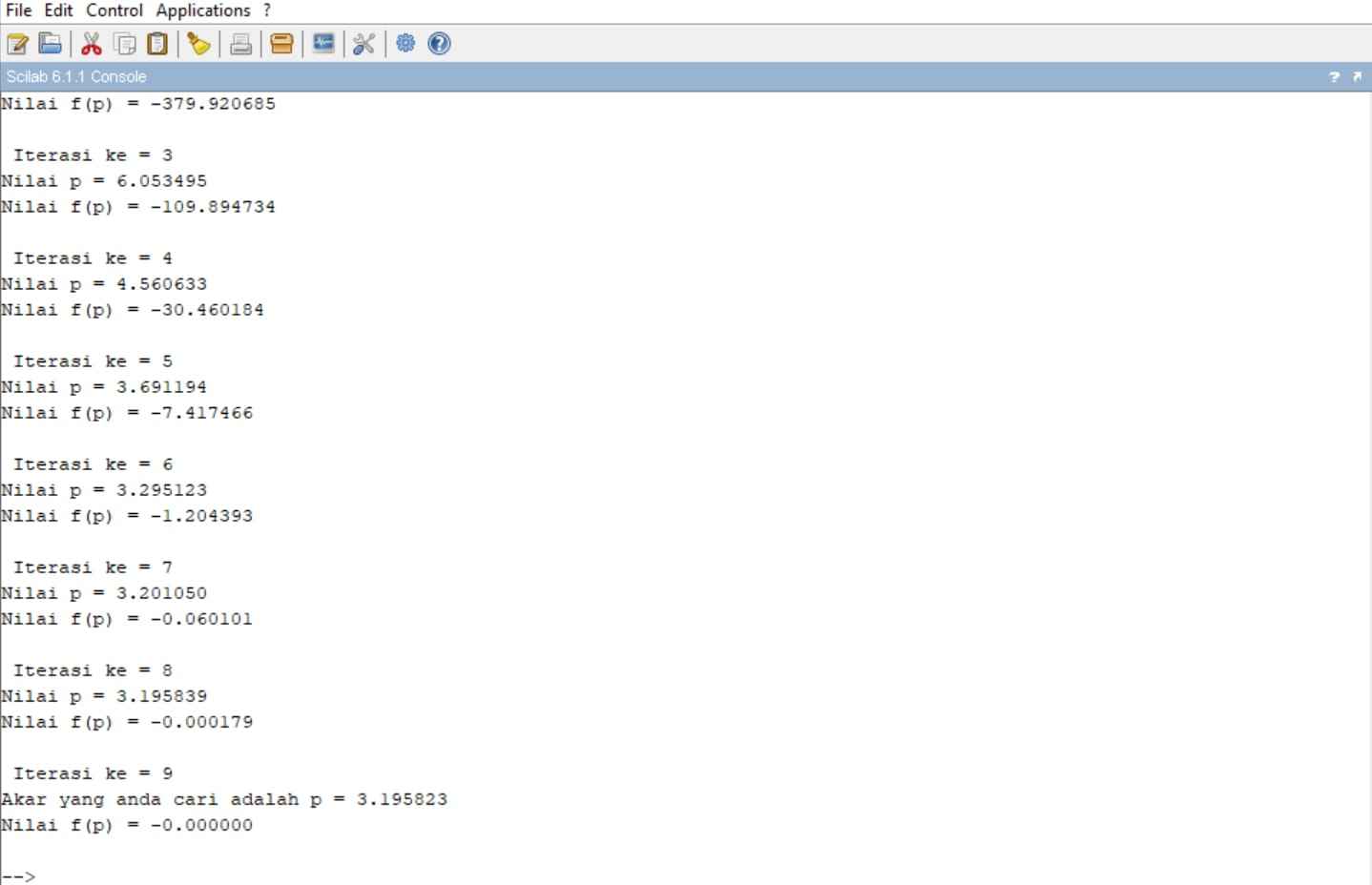
Perhitungan menggunakan aplikasi Scilab :