Metode Numerik merupakan suatu teknik yang digunakan untuk memformulasikan persoalan matematika sehinga dapat diselesaikan dengan menggunakan operasi aritmatika biasa. Pada umumnya metode numerik digunakan untuk menyelesaikan persoalan matematika yang tidak dapat diselesaikan dengan metode analitik biasa.Dalam Metode Numerik kita mengenal dua buah jenis sistem persamaan yaitu Sistem Persamaan Linier dan Sistem Persamaan Non-Linier. Masing-masing sistem persamaan memiliki beberapa metode. Dalam Sistem Persamaan Linier diantara metodenya adalah metode Eliminasi Gauss, metode Eliminasi Gauss-Jordan, metode Dekomposisi LU (Lower-Upper). Dan untuk Sistem Persamaan Non-Linier diantara metodenya adalah metode Bisection (Bagi-Dua), metode Regula Falsi, metode Newton Raphson, metode Secant, dan metode Fix Iteration. Pada kesempatan kali ini membahas tentang 2 buah metode yang ada dalam Sistem Persamaan Non-Linier, yaitu metode Titik Tetap dan metode Regula Falsi. Dan proses pembandingan ini menggunakan perangkat bahasa pemrograman scilab, hal ini untuk memudahkan dalam hal analisis algoritma penyelesaian metode, dan monitoring dalam hal waktu eksekusi dan analisis hasil output

Metode Iterasi titik Tetap

Metode iterasi titik tetap disebut juga metode iterasi sederhana, metodelangsung, atau metode substitusi beruntun.Metode iterasi titik tetap adalahmetode yg memisahkan x dengan sebagian x yang lain sehingga diperoleh : x =g(x)

 

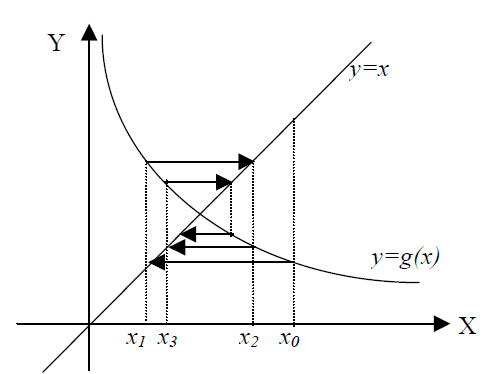
Kesederhanaan metode ini karena pembentukan prosedur iterasinya yangmudah dibentuk sebagai berikut : 

1.  Susunlah persamaan f (x) = 0 menjadi bentuk x = g(x). Lalu bentuklah menjadi prosedur iterasi :

x_n+1 = g ( x )

2. tentukan nilai awal x₀

3. Lakukan iterasi dengan menghitung nilai x = g ( x ), x = g ( x ), x = g ( x )... yang mudah-mudahan konvergen keakar sejati k, sehingga : 

f ( k ) = 0  : k = g ( k )

4. Cek konvergensi terhadap XTOL ( jika ada)

Berikut ini adalah contoh program Scilab untuk mencari akar persamaan x^2 - 2x-3 = 0 menggunakan metode iterasi titik tetap epsilon = 0,00001 dan x₀ = 4:

Program scilab

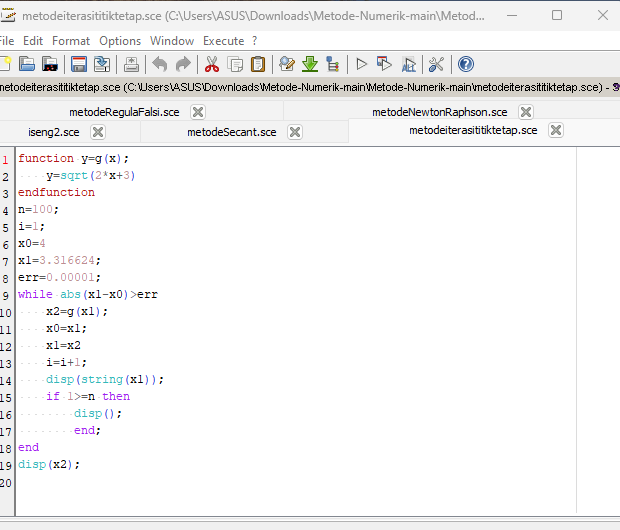
Hasil Scilab

 

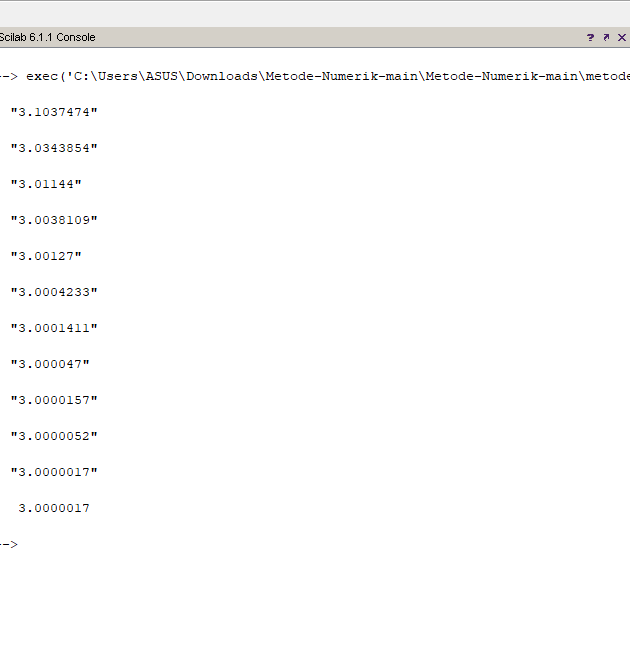
Metode Regulasi Falsi

Metode regula falsi disebut juga metode Interpolasi Linear atau metodePosisi Salah adalah metode yang digunakan untuk mecari akar-akar persamaannonlinear melalui proses iterasi. Metode regula falsi merupakan metode pencarian akar persamaan dengan memanfaatkan kemiringan dan selilih tinggidari dua titik batas range. Solusi akar (atau akar-akar) dengan menggunakanmetode Regula Falsi merupakan modifikasi dari Metode Bisection dengan caramemperhitungkan ‘kesebangunan’ yang dilihat pada kurva berikut:

 

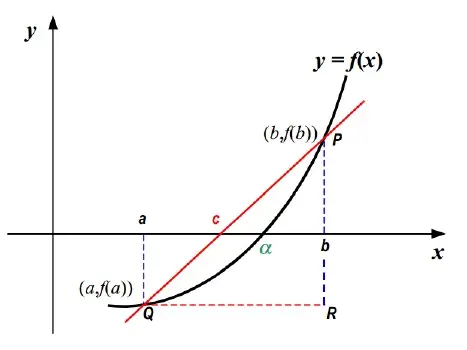
Kesederhanaan metode ini karena pembentukan prosedur iterasinya yangmudah dibentuk sebagai berikut :

1. Tentukan nilai awal a dan b

2. Cek konvergensi a dan b

3. Lakukan iterasi

4. Hitung nilai c diantara a dan b, dimana :

c = a .f ( b ) - b . f ( a ) / f ( b ) - f ( a )     5. Cek Konvergensi nilai c   Berikut ini adalah contoh program Scilab untuk mencari akar persamaan x^2 - 1-sin(x) = 0 menggunakan metode regulasi falsi

 

Program Scilab 

 

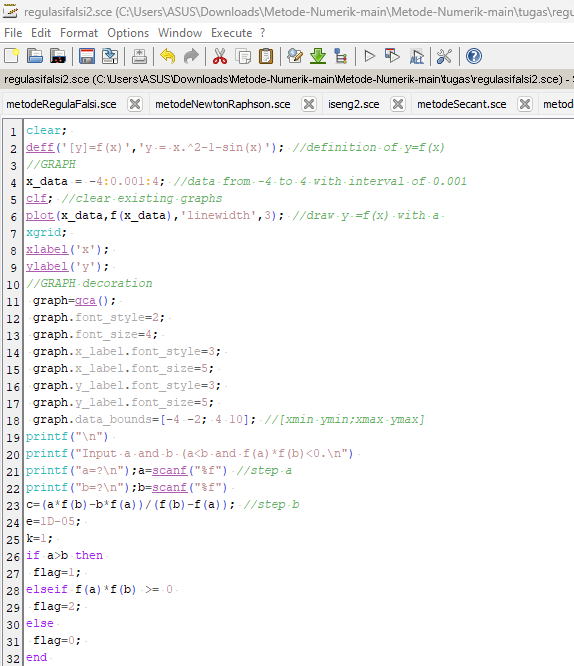
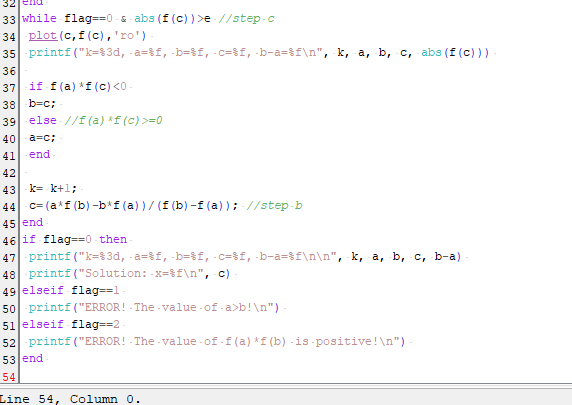
Hasil Program & Grafik

 

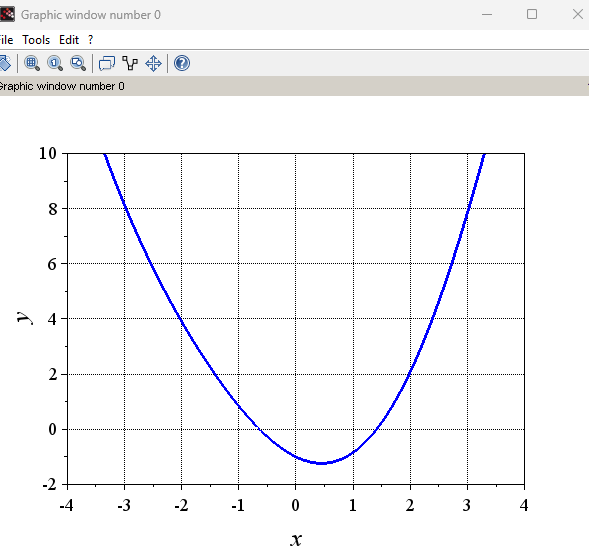
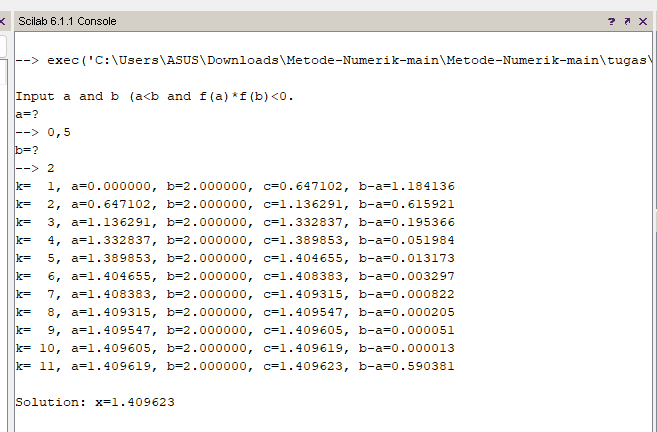
kesimpulannya, metode iterasi titik tetap dan regulasi falsi merupakan teknik yang efektif dan efisien untuk menyelesaikan berbagai masalah matematika dan keilmuan lainnya. Dengan menggunakan bahasa pemrograman Scilab, kita dapat menerapkan kedua metode ini secara mudah dan akurat. Dengan demikian, Scilab memberikan solusi yang andal bagi para ilmuwan dan praktisi dalam menyelesaikan perhitungan numerik yang kompleks.

Model matematika sangat dibutuhkan untuk memecahkan masalah dalam berbagai disiplin ilmu pengetahuan; bidang fisika, kimia, ekonomi, bidang rekayasa atau teknik. Model matematika yang disedehanakan dan linier sering tidak representatif untuk diaplikasikan dalam desain. Oleh karena itu dibutuhkan solusi numerik untuk persamaan non-linier agar dapat diaplikasikan secara nyata pada bidang desain. Pada kesempatan kali ini, saya akan membahas dua metode numerik yaitu Metode Newton-Raphson dan Metode Secant. Kedua metode ini sangat berguna dalam menyelesaikan persamaan matematika yang sulit atau tidak dapat diselesaikan secara analitik. Dalam pembahasan kali ini, saya akan menggunakan software Scilab untuk mengimplementasikan kedua metode tersebut.

Scilab adalah salah satu software open-source untuk pengolahan data numerik dan ilmiah. Scilab memiliki fitur-fitur yang sangat lengkap dan dapat digunakan untuk berbagai macam keperluan seperti pengolahan data, analisis numerik, dan simulasi. Scilab dapat digunakan di berbagai sistem operasi seperti Windows, Linux, dan Mac OS.

METODE NEWTON RAPSHON

Metode Newton Rapshon merupakan metode pendekatan yang menggunakan satu titik awal dan mendekatinya dengan memperhatikan gradien pada titik tersebut. Metode ini dimulai dengan mencari garis singgung kurva pada titik tersebut Metode ini dimulai dengan mencari garissinggung kurva pada titik (x_i,f(x_i)). Perpotongan garis singgung dengansumbu x yaitu X_i+1, akan menjadi nilai x yang baru, dengan cara dilakukan berulang-ulang (iterasi).

 

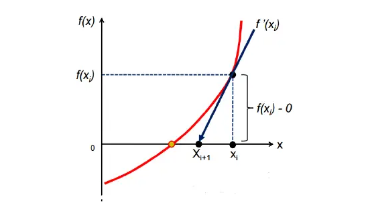
Telah diketahui bahwa gradien garis singgung kurva adalah turunan  pertama dari kurva tersebut, yaitu f' (x_i). Sehingga persamaan garis singgungnya:

f (x_i) - y f'(x_i) - (x_i - x)

Garis ini melalui titik (x_i+1,0), maka didapat :

• f(x_i)-0 = f'(x_i)(x_i - x_i+1)
• f(x_i)/f(x_i) = (x_i - x_{i +1})
• x_i+1 = x_i - f(x_i) / f'(x_i)

X_i+1 digunakan untuk menaksir nilai akar dari f(x) dan pendekatanyang lebih baik untuk akar dari f(x). Metode ini banyak digunakan untuk akardari suatu persamaan.

Algoritma Metode Newton Rapshon :

1.Tentukan nilai awal x₀

2. Hitung f (x₀) kemudian cek konvergensi f (x₀)

3. Tentukan fungsi f₀(x₀), kemudian hitung f₀(x₀)

4. Lakukan iterasi

5. Hitung nilai taksiran akar selanjutnya:

x_n+1 = x_n - f ( x_n ) /  f'( x_n )

6. Cek nilai Konvergensi terhadap XTOL ( jika ada )

Untuk mengimplementasikan metode Newton-Raphson pada program Scilab, kita dapat membuat sebuah fungsi yang merepresentasikan f(x) dan sebuah fungsi yang merepresentasikan f'(x). Kemudian, kita dapat menggunakan algoritma yang sudah dijelaskan di atas. Berikut adalah contoh implementasi Metode Newton-Raphson pada Scilab:

 

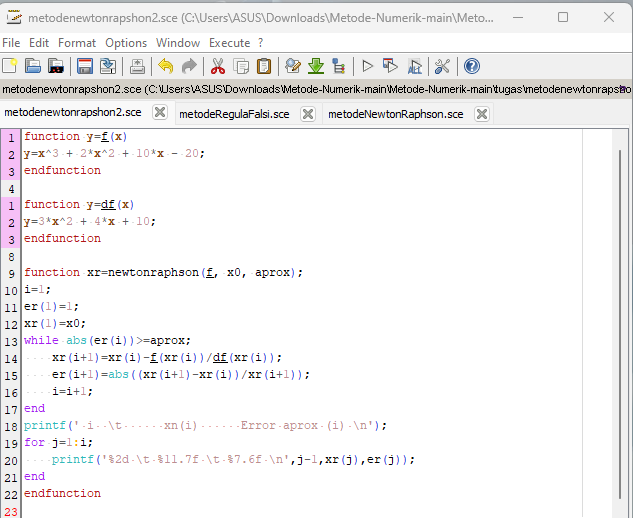
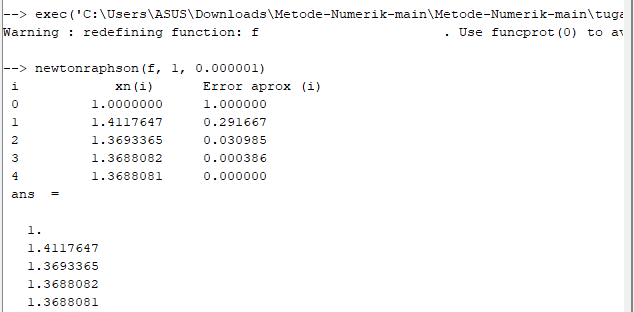
 caranya:-execute-ketik: newtonraphson(f, 1, 0.000001)

Program ini akan mencari solusi untuk persamaan x³ + 2x² + 10x - 20 = 0 dengan nilai awal x0 = 1 dan kriteria konvergensi tol = 0,000001. Hasilnya akan ditampilkan di layar. Metode numerik Newton-Raphson adalah salah satu metode yang berguna untuk menyelesaikan persamaan nonlinear. Dalam Scilab, implementasinya relatif mudah dan cepat.

METODE SECANT

Metode secant merupakan salah satu metode terbuka untuk menentukan solusi akar dari persamaan tak lienar, dengan prinsip utama sebagai berikut:

1. Metode ini melakukan pendekatan terhadap kurva f (x) dengan garissecant yang ditentukan oleh dua titik terakhir.

2. Nilai taksiran akar selanjutnya adalah titik potong antara garis secant dengan sumbu X.

Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimanakemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.

 

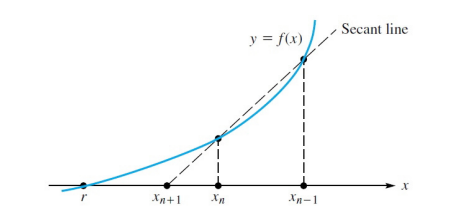
f’ (X) =( f (X_n) – f (X_n-1)) / (X_n – X_n-1)

X_n+1 = X_n – ( (f(X_n) (X_n – X_n-1)) / ( f(X_n) -f(X_n-1) )

Algoritma Metode Secant

1. Tentukan nilai awal x0 dan x1

2. Hitung f (x0) dan f (x1) kemudian cek konvergensi f (x0) dan f (x1)

3. Lakukan iterasi

4. Hitung nilai taksiran akar selanjutnya

Xn+1 = Xn – ( (f(Xn) (Xn – Xn-1)) / ( f(Xn) -f(Xn-1) )

5. Cek konvergensi terhadapa XTOL (Jika ada)

Berikut adalah contoh implementasi Metode Secant pada Scilab :

 

 

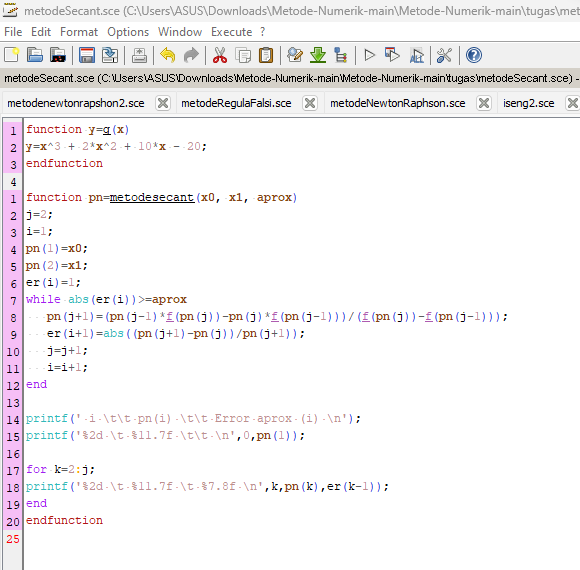
caranya:

-execute

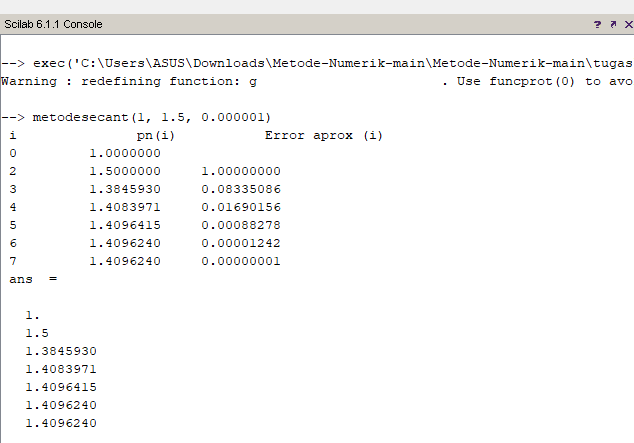
-ketik: metodesecant(1, 1.5, 0.000001)

Program ini akan mencari solusi untuk persamaan x3 + 2x2 + 10x - 20 = 0 dengan nilai awal x0 = 1,5 dan kriteria konvergensi tol = 0,000001. Hasilnya akan ditampilkan di layar. Metode numerik Newton-Raphson adalah salah satu metode yang berguna untuk menyelesaikan persamaan nonlinear. Dalam Scilab, implementasinya relatif mudah dan cepat.

Secara keseluruhan, metode Newton-Raphson dan metode Secant adalah metode numerik yang sangat berguna dalam menyelesaikan masalah matematika dan sains lainnya. Dalam bahasa pemrograman Scilab, implementasi kedua metode ini sangatlah mudah dan efisien, sehingga para ilmuwan dan praktisi dapat dengan mudah menggunakannya untuk menyelesaikan perhitungan numerik yang rumit. Dengan demikian, Scilab adalah pilihan yang tepat untuk menyelesaikan masalah numerik dalam berbagai bidang ilmu pengetahuan dan teknik.